Study Guide 11 - Mechanics of Biological Systems: Rotaional Motion
- A bird goes into a flight pattern which involves a semi-circular path at the bottom. The semicircle has a radius of \(\mathrm {20 \;m.}\) The bird's mass is \(\mathrm {0.50 \;kg.}\) The bird has a constant speed of \(\mathrm {10\;m \;s^{-1}.}\)
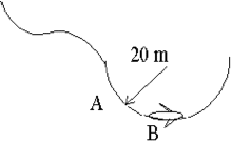
a) What is the magnitude of the net force on the bird at point A? What is the force called centripetal force or centrifugal force?
The bird travels in a circle because there is a net force toward the centre of the circle called the centripetal force.
The centripetal force which is given by:
\(\mathrm {f_c = mv^2/r}\)
where r is the radius of the circle and m is the mass of the object and v is its tangential velocity.
\(\mathrm {f_c = mv^2/r = 0.5(10^2)/20 = 2.5\; N}\)
b) What is the magnitude of the net force on the bird at point B?
The net force on the bird is the same at all points of the circle if the velocity is constant so the answer is the same as for part (a)
c) What is the magnitude of the upward force exerted on the bird at point B?
Since the net force on the bird is the same at every part of the circle, at the bottom the air must exert an upward lift force \(\mathrm {(f_L)}\) to provide this centripetal force and support the weight of the bird.
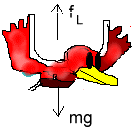
\(\mathrm {f_c = f_L - mg}\)
\(\mathrm{f_L = f_c + mg = 2.5 + 0.5(9.8) = 7.4\; N}\)
- A stone on the end of a 1.50 m string is rotating in a horizontal circle. The string breaks and the stone flies off at a tangent when its speed is 20.0 m/s. What was the tension in the string at the breaking point? The stone's mass is 0.500 kg.
The centripetal force is:
(A) \(\mathrm {F = m/(v^2/r)}\)
(B) \(\mathrm {F = mv^2/r}\)
(C) \(\mathrm {F = m\omega^ 2r}\)
(D) \(\mathrm {F = m\omega ^2/r}\)
(E) \(\mathrm {F = m/\omega ^2r}\)
(B) \(\mathrm {F = mv^2/r}\)
The centripetal force:
(A) is supplied by the Earth's gravitational force
(B) is a fundamental force that appears whenever objects move in circles
(C) is provided by the tension in the string
The centripetal force is provided by the tension in the string. Using:
\(\mathrm {F = mv^2/r = 0.5 \times 20^2/1.5 = 133\; N}\)
- The \(\mathrm{100\; kg}\) man and the \(\mathrm{750\; N}\) scaffold are supported by cables with tensions \(\mathrm {T_1}\) and \(\mathrm {T_2.}\) Determine
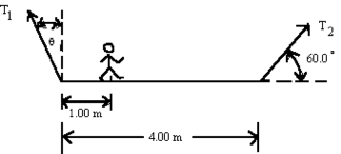
(a) \(\mathrm {T_2}\)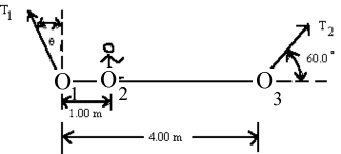
Moments can be taken about any point but if \(\mathrm{T_2}\) is wanted which is the best point to choose in this problem?
Taking moments about \(\mathrm{O_1}\) makes the unknown \(\mathrm {T_1}\) disappear from the problem.
Take moments about \(\mathrm {O_1}\) and set their sum equal to zero.
Counter-clockwise torque produced by \(\mathrm {T_2}\) is \(\mathrm{T_2 \times 4.00\; \sin\; 60 = 3.464 \;T_2}\)
See diagram below: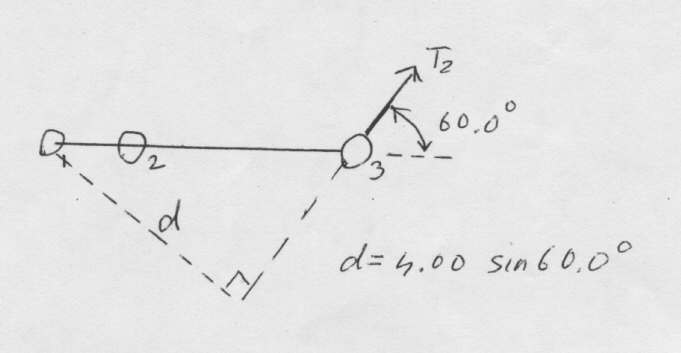
Clockwise torque produced by the weight of the scaffold (acting at its centre) and the weight of the man i.e.,
\(\mathrm {(750)(2.00) + (100)(9.8)(1.00) = 2480}\)
(Be careful to note that the weight of the scaffold in N is given but the mass of the man in kg is given)\(\mathrm {\sum \tau = 0 \\ 3.464\; T_2 - 2480 = 0 \\ T_2 = 2480/3.464 = 716\; N}\)
(b) \(\mathrm {T_1}\)Using moments, the value of T2 was found in Part (a)
The value was \(\mathrm {716\; N}\)
Now \(\mathrm{\sum F_x = 0}\) and \(\mathrm {\sum F_y = 0}\) can be used to find the other two unknowns \(\mathrm{T_1}\) and \(\mathrm {\theta.}\)\(\mathrm{T_2\; \cos \;60 - T_1\; \sin \theta = 0 \;or \\ T_1 \; \sin \theta = T_2\; \cos \;60 = 358 \qquad [1]}\)
\(\mathrm{T_2\; \sin \;60 + T_1\cos \theta - 100(9.8) - 750 = 0 \;or \\ T_1\cos \theta = - T_2\; \sin \;60 + 980 + 750 = 1110 \qquad [2]}\)
Divide [1] by [2]
\(\mathrm{\tan \theta = 358/1110 =0.322 \\ \theta = 17.9^\circ \; {\color {red} {This\; is \;the\; answer\; to\; part\; (c)}}}\)
Use either [1] or [2] to find \(\mathrm{T_1}\)
Using [1]
\(\mathrm{T_1 = 358/\sin 17.9 = 358/0.307 = 1170\; N}\)
(c) \(\mathrm{\theta}\)Using moments, the value of T2 was found in Part (a)
The value was \(\mathrm {716\; N}\)
Now \(\mathrm{\sum F_x = 0}\) and \(\mathrm {\sum F_y = 0}\) can be used to find the other two unknowns \(\mathrm{T_1}\) and \(\mathrm {\theta.}\)\(\mathrm{T_2\; \cos \;60 - T_1\; \sin \theta = 0 \;or \\ T_1 \; \sin \theta = T_2\; \cos \;60 = 358 \qquad [1]}\)
\(\mathrm{T_2\; \sin \;60 + T_1\cos \theta - 100(9.8) - 750 = 0 \;or \\ T_1\cos \theta = - T_2\; \sin \;60 + 980 + 750 = 1110 \qquad [2]}\)
Divide [1] by [2]
\(\mathrm{\tan \theta = 358/1110 =0.322 \\ \theta = 17.9^\circ \; {\color {red} {This\; is \;the\; answer\; to\; part\; (c)}}}\)
Use either [1] or [2] to find \(\mathrm{T_1}\)
Using [1]
\(\mathrm{T_1 = 358/\sin 17.9 = 358/0.307 = 1170\; N}\)
- AB is a uniform beam of weight 400 N and length 10.0 m. AC is 6.00 m. A 1000 N load is suspended from B. What is the magnitude of the tension T?
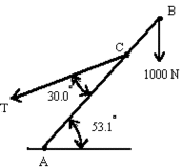
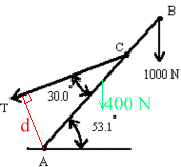
Taking moments about A
\(\mathrm{Td - 400(5 \; \cos \; 53.1) - 1000(10\; \cos \;53.1) = 0}\)
\(\mathrm {T(6\; \sin \;30) = 400(5 \times 0.6) + 1000(10 \times 0.6)}\)\(\mathrm{T(6 \times 0.5) = 1200 + 6000 = 7200}\)
\(\mathrm {T = 7200/3 = 2400\; N}\)
- A lab technician is centrifuging a blood sample at an angular speed of 3000 rpm. The radius of the circular path followed by the sample is 0.250 m.
(a) Find the speed of the sample in m/s.The relationship between speed, angular velocity and radius is: \(\mathrm {v = r\omega}\)
\(\mathrm {3000\; rpm\; must\; be\; expressed\; in\; rad/s \\ 3000\; rpm = 3000(2\pi )/60 = 314\; rad/s \\ v = r\omega = 0.25 \times 314 = 78.5\; m/s}\)
(b) If it reaches this angular speed in 3.00 minutes, what is the angular acceleration in \(\mathrm {rad/s^2?}\)Which is the appropriate equation to use in this problem? Note that all of the following are correct equations.
(A) \(\mathrm {\omega = \omega_0 + \alpha t}\)
(B) \(\mathrm {\omega = \omega_0 + \omega_0t + ½\alpha t^2}\)
(C) \(\mathrm {\omega^2 = \omega_0{^2} + 2\alpha \theta}\)
In part (a) we calculated that the final angular velocity was 314 rad/s
\(\mathrm {\omega = \omega_0 + \alpha t}\)\(\mathrm {314 = 0 + \alpha (3 \times 60)}\)
\(\mathrm {\alpha = 1.75\; rad/s^2}\)
- A flywheel rotating at 6000 rpm is brought to rest while turning through 500 revolutions.
(a) What is the angular acceleration?Which is the appropriate equation to use in this problem? Note that all of the following are correct equations.
(A) \(\mathrm {\omega = \omega_0 + \alpha t}\)
(B) \(\mathrm {\omega = \omega_0 + \omega_0t + ½\alpha t^2}\)
(C) \(\mathrm {\omega^2 = \omega_0{^2} + 2\alpha \theta}\)
\(\mathrm {\omega^2 = \omega_0{^2} + 2\alpha \theta}\)
\(\mathrm {\omega = 6000\; rpm = 6000(2\pi )/60 = 200\pi \; rad/s \\ \theta = 500\; rev = 500(2\pi) = 1000\pi \; rad \\ 0 = (200\pi)^2 + 2\alpha(1000\pi) \\ \alpha = -20\pi \;rad/s^2}\)
(b) How long does it take to come to rest?Which is the appropriate equation to use in this problem? Note that all of the following are correct equations.
(A) \(\mathrm {\omega = \omega_0 + \alpha t}\)
(B) \(\mathrm {\omega = \omega_0 + \omega_0t + ½\alpha t^2}\)
(C) \(\mathrm {\omega^2 = \omega_0{^2} + 2\alpha \theta}\)
Either of the equations
\(\mathrm {\omega = \omega_0 + \alpha t}\)
\(\mathrm {\omega = \omega_0 + \omega_0t + ½\alpha t^2}\)can be used as they both involve t. We will use the first.
In part (a) we calculated that \(\mathrm {\alpha = - 20\pi \; rad/s^2 \;and\; \omega_0 = 200\pi \; rad/s}\)
\(\mathrm {0 = 200\pi - 20\pi t}\)
\(\mathrm {t = 10 \;s}\)
- Two rods of negligible mass are 2.00 m long. Each have masses totalling 5.00 kg distributed along the rod as shown. What are the moments of inertia about end O for each rod?
(a)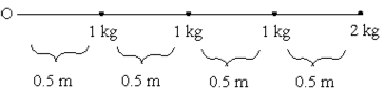
The moment of inertia is given by
\(\mathrm {I = \sum mr^2}\)
\(\mathrm {I = 1 \times 0.52 + 1 \times 12 + 1 \times 1.52 + 2 \times 22 = 0.25 + 1 + 2.25 + 8 = 11.5 \;kg\; m^2}\)
(b)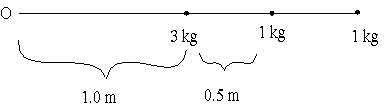
The moment of inertia is given by
\(\mathrm{I = \sum mr^2}\)
\(\mathrm {I = 3 \times 12 + 1 \times 1.52 + 1 \times 22 = 3 + 2.25 + 4 = 9.25\; kg\; m^2}\)
- A solid cylinder \(\mathrm {(M = 12.0\; kg)}\) rotates about an axis through its centre as in text Example 9-9. A rope is wrapped several times around the cylinder and is pulled with a force of magnitude \(\mathrm {150\; N}\). It acquires an angular acceleration of \(\mathrm {15.0\; rad/s^2}\) in a time of 1.50 min. It starts from rest.
(a) What is the radius of the cylinder?The rotational equivalent of Newton's 2nd law is
\(\mathrm {\sum \tau = I \alpha}\)\(\mathrm {For\; a\; uniform\; cylinder\; of\; radius\; r\; and\; mass\; m, I = ½mr^2}\)
\(\mathrm {150\; r = ½mr^2 (15) = ½(12)r^2 (15)}\)
\(\mathrm {r = 10/6 = 1.67 \;m}\)
(b) What is the moment of inertia of the cylinder?\(\mathrm {For\; a\; uniform\; cylinder\; of\; mass\; m\; and\; radius\; r, I = ½mr^2}\)
\(\mathrm {In\; part\; (a)\; it\; was\; determined\; that\; r = 1.67\; m}\)
\(\mathrm {Therefore\; I = ½(12)(1.67)^2 = 16.7\; kg\; m^2}\)
(c) What length of rope unwinds from the cylinder?Find the total angle turned through in \(\mathrm {1.5 \;min = 90\; s}\)
\(\mathrm {\theta =\theta_0 + \omega_0t + ½\alpha t^2}\)\(\mathrm {\theta = 0 + 0t + ½(15)(90)^2 = 60750 \;rad}\)
\(\mathrm {Length\; of\; rope = distance\; of\; circumference\; traced\; out = r\theta = 1.67(60750 = 1.01\times 105 \;m)}\)
- Masses of 1.00 kg are at each end of a rod of negligible mass and length 2.00 m. The rod is rotated in a horizontal plane about its centre. What is the rotational kinetic energy of the system when the rod is rotating at 150 rpm?
The moment of inertia of the rod and masses rotated about the centre is \(\mathrm{I = \sum r^2 = 1(1)^2 + 1(1)^2 = 2\; kg\; m^2}\)
\(\mathrm {\omega = 150(2\pi)/60 = 15.7\; rad/s}\)
\(\mathrm {KE = ½I\omega^2 = ½(2)(15.7)^2 = 247\; J}\)
- A thin walled hoop of radius r and mass m rolls from rest without slipping down an incline of height 15.0 m. What is the speed at the bottom?
For a thin hoop \(\mathrm {I = mr^2}\)
From conservation of energy\(\mathrm {PE = KE_{trans} + KE_{rot}}\)
\(\mathrm{mgh = ½mv^2 + ½I\omega^2 = ½mv^2 + ½(mr^2)\omega^2 = ½mv^2 + ½(mr^2)(v/r)^2 = ½mv^2 + ½mv^2 = mv^2}\)
\(\mathrm{Therefore\; gh = v^2}\)
\(\mathrm{v = (gh)^{1/2} = (9.8 \times 15)^{1/2} = 12.1\; m/s}\)
- A figure skater is rotating at \(\mathrm {2.0\; rps}\) (revolutions per second) with an angular momentum of \(\mathrm {14\; kg\; m^2 s^{-1}.}\)
(a) What is her rotational K.E.?\(\mathrm {2\; rps = 4\pi \; rad/s}\)
\(\mathrm {L = I\omega = I(4\pi) = 14 \\ Therefore\; I = 14/(4\pi) kg\; m^2}\)\(\mathrm {KE = ½I\omega^2 = [½(14)/(4\pi)](4\pi)2 = 88\; J}\)
(b) The skater extends her arms, increasing her moment of inertia by 20%. What is her new rotational K.E.?In order to solve part (b) it is useful to have the solution to part (a) handy
I increases by 20% but momentum is conserved
\(\mathrm{I\omega = I'\omega' = 1.2\; I\omega' \\ \omega' = \omega /1.2}\)
\(\mathrm {KE' = ½I'\omega'^2 = ½(1.2 I)(\omega /1.2)^2 = ½I\omega^2(1/1.2)}\)
\(\mathrm {But\; ½I\omega^2 = 88\; J, the\; original\; KE}\)
\(\mathrm{Therefore\; KE' = 88/1.2 = 73 \;}\)
- A uniform flywheel is mounted on an axle through its centre. A tangential force of 100 N acts for 1.00 minute. What is the angular momentum of the wheel at the end of this time? The wheel has a mass of 10.0 kg and a radius of 1.00 m.
The mass of the wheel is irrelevant.
The change in momentum of the wheel is equal to the product of the moment and the time
i.e., \(\mathrm {\Delta L = \tau t = (100 \times 1) (60) = 6.0\times 10^3 \;kg\; m^2/s}\)Alternatively if I is the moment of inertia of the wheel then
\(\mathrm {\tau = I \alpha}\)\(\mathrm {\alpha = (100 \times 1)/I}\)
\(\mathrm {\omega = \omega_0 + \alpha \;t = 0 + (100/I)(60) = 6.0\times 10^3/I}\)
\(\mathrm {L = I\omega = I(6.0\times 10^3)/I = 6.0\times 10^3 \;kg \;m^2/s \;as \;before}\)








