Biophysics Textbook Questions - Chapter 10

(a) \(\text{(tensile) strain} \; \varepsilon = \frac{\Delta \ell}{\ell _o} = \frac{9.00 \times 10^{-2}\; \text m}{26.0 \; \text m} = 3.46 \times 10^{-3} \quad (3.46_2 \times 10^{-3})\)

(b) \(\text{(tensile) stress} \; \tau = \frac{F}{A} = \frac{mg}{\pi r^2}\)

\(\therefore \tau = \frac{(79.0\; \text{kg})(9.80\; \text{m/s}^2)}{\pi (4.50 \times 10^{-3}\text m)^2} = 1.22 \times 10 ^7\frac{\text N}{\text m^2} \quad \bigg( 1.21_7 \times 10^7 \frac{\text N}{\text m^2}\bigg)\)

(c) \(y = \frac{\tau}{\varepsilon} = \frac{1.21_7 \times 10^7 \text {N/m}^2}{3.46_2 \times 10^{-3}}= 3.52 \times 10^9 \text {N/m}^2\)

(a)

 \(\frac{F}{A} = Y \frac{\Delta \ell}{\ell _o} \therefore \Delta \ell = \frac{F \ell _o}{YA} = \frac{m\;g\; \ell_o}{YA} \\ \therefore \Delta \ell = \frac{(1.10\; \text{kg})(9.80\; \text{m/s}^2)(0.650\; \text m)}{(2.00 \times 10^7\;  \text {N/m} ^2)(3.00 \times 10^{-6}\text m^2)}= 0.117 \text m \\ \therefore \ell = \ell_o + \Delta \ell = (0.650 + 0.117) \text m = 0.767 \text m\)

(b)

\(\text{Similar to (a), except that } \; g = 2.00\; \text {m/s}^2 \\ \Rightarrow \Delta \ell = 0.024\; \text m\\ \Rightarrow \ell = 0.674\; \text m\)

\(\frac{F}{A} = Y \frac{\Delta \ell}{\ell_o} \quad \therefore \text{For const.} \; F, Y, \&\; \ell_o : \Delta \ell \propto \frac{1}{A} \\ \therefore \; \frac{\Delta \ell_2}{\Delta \ell _1} = \frac{A_1}{A_2} \; \text {or} \; \Delta \ell _2 = \Delta \ell _1 \frac{A_1}{A_2} \\ \therefore \; \Delta \ell_2 = 0.120 \; \text{mm} \times \frac{1}{2} = 0.0600 \; \text{mm}\)

\(\begin {align} \frac{F}{A} &= Y \frac{\Delta \ell}{\ell _o} \; \therefore \; F = \frac{YA \Delta \ell}{\ell_o}= \frac{Y \pi r^2 \Delta \ell}{\ell_o} \\ r &= \frac{2.50\; \text{cm}}{2}= 1.25 \times 10^{-2} \text m \\ \frac{\Delta \ell}{\ell _o} &= 0.0100\; \% = 0.0100 \times \frac{1}{100} = 1.00 \times 10^{-4}\\ \therefore \; F &= (2.00 \times 10 ^{11} \; \text {N/m}^2) \pi (1.25 \times 10^{-2} \text m)^2(1.00 \times 10^{-4})\\ &= 9.82 \times 10^3 \text N \end {align}\)

\(\begin {align} \frac{F}{A} = Y \frac{\Delta \ell}{\ell _o}\; \therefore \; Y & = \frac{F \ell_o}{A \Delta \ell} \\ \therefore \; \text {if} \; F = 24.0 \text N, \; Y &= \frac{(24.0 N)(0.190 \text m)}{(12.0 \times 10 ^{-4} \text m^2)(2.80 \times 10^{-2} \text m)} \\ & = 1.36 \times 10 ^5 \; \text {N/m}^2 \quad (1.35_7 \times 10^5 \text {N/m}^2) \end {align}\)

If \(F = 480 \; \text N, \Delta \ell \) is the same as above (and \(\ell_o\) and \(A\) are the same).

\(\therefore \; Y \propto F \; \therefore \;\frac{Y_2}{Y_1} = \frac{F_2}{F_1} \\ \therefore \; Y_2 = Y_1 \frac{F_2}{F_1} = 1.35_7 \times 10^5 \text {N/m}^2 \times \frac{480\; \text N}{24.0\; \text N}= 2.71 \times 10^6 \frac{\text N}{\text m^2}\)

When standing erect, a person's weight is supported chiefly by the larger of the two leg bones. Assuming this bone to be a hollow circular tube of \(2.5 \; \text {cm}\) internal diameter and \(3.5 \ \text{cm}\) external diameter, what compressive load must this bone (in each leg) carry in the case of a \(70\; \text{kg}\) person?

First of all, you must make a diagram of the cross-section of the bone. Draw a diagram on a piece of paper.

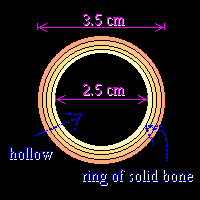
Remember that the \(70\; \text{kg}\) represents the person's mass, and thus is not a force.

Calculate the downward force.

You should have had: \(\text{downward force } = 70\; \text{kg} \times 9.8\; \text{m/s}^2 = 686\; \text N\)

Now calculate the cross-sectional area of the bone.

Remember that the area of a circle is \(A = \pi r^2\)

Cross-sectional area, we'll call '\(A\)' is:

\(\begin {align} A & = \pi (3.5/2)^2 - \pi (2.5/2)^2 \\ &= 9.62 - 4.91 \\ &= 4.71\; \text{cm}^2 \\ &= 4.71 \times 10^{-4} \; \text{m}^2 \end {align}\)

Now calculate the compressive load -- that is, the force per unit area of bone. Remember that there are two bones, each carrying an equal share of the load.

Compressive load, we'll call 'CL' is:

\(\begin {align} CL & = \frac{\text{force}}{\text{unit area of bone}} \\ & = \frac{686 \; \text N}{2 \times 4.71 \times 10^{-4}}\\ & = 7.3 \times 10^5 \; \text {Nm} ^2 \end {align}\)

If the leg bones described in question 10-6 are \(90\; \text{cm}\) long, what is the amount of compression in each leg at the fracture point? Assume that the leg bones remain elastic under compression until fracture, which occurs at a stress of \(1.4 \times 10^8\; \text {N/m}^2.\)

Hooke's Law applies in compression (as in this problem) as well as in tension.

\(\begin {align} stress & = Y \; strain \\ & = \frac{y \Delta L}{L} \end {align}\)

From your text, \(Y = 2 \times 10^{10} N \text m^2.\)

You should be able to substitute and calculate the change of length now. (In the above formula, L is the leg length)

The stress was given in the problem, and the leg length is \(0.9\; \text m.\)

You should have found that \(L = 0.0063\; \text m.\)

(a)

\(\begin {align} \tau &= Y \varepsilon \; \text {or} \; \frac{F}{A} = Y \varepsilon \; \therefore \; \varepsilon = \frac{F}{AY} = \frac{mg}{\pi (r_o{^2}- r_i{^2})Y} \\ \therefore \; \varepsilon & = \frac{(65.0 \; \text{kg})(9.80 \; \text{m/s}^2)}{\pi [(1.05 \times 10^{-2} \text m)^2- (0.430 \times 10^{-2}\text m)^2](1.40 \times 10^{10}\; \text {N/m}^2)} \\ &= 1.58 \times 10^{-4} \quad (1.57_8 \times 10^{-4}) \end {align}\)

(b)

\(\varepsilon = \frac{\Delta \ell}{\ell _o} \; \therefore \; \Delta \ell = \varepsilon \; \ell_o = (1.57_8 \times 10^{-4})(0.330\; \text m) = 5.21 \times 10^{-5} \text m\)

\(\frac{F}{A} = Y \frac{\Delta \ell}{\ell_o} \; \therefore \frac{mg}{A} = Y \frac{\Delta \ell}{\ell_o} \\ \text {Given:} \; \frac{\Delta \ell}{\ell_o} = 6.50 \times 10^{-3} \% = 6.50 \times 10^{-3} \times \frac{1}{100}= 6.50 \times 10^{-5} \\ \therefore \; \frac{(10.0 \; \text{kg})(9.80 \; \text{m/s}^2)}{1.40 \times 10^{-4}\text m^2}= Y \; (6.50 \times 10^{-5}) \\ \therefore \; Y = 1.08 \times 10^{10} \; \text {N/m}^2\)

(a)

\(\begin {align} \text{At proportion limit, }\; \tau & = (1.50 \times 10^{-3})Y\\ & = (1.50 \times 10^{-3})(2.00 \times 10^{11} \; \text {N/m}^2) \\ & = 3.00 \times 10 ^8 \; \text {N/m}^2 \end {align}\)

\(\tau = \frac{F}{A} = \frac{w}{A} \quad (\text {where}\; w = \text{weight}) \\ \therefore \; w = \tau A = (3.00 \times 10^8 \frac{\text N}{\text m^2})(0.0450 \;\text m^2)= 1.35 \times 10^7 \; \text N\)

(b)

\(\tau = Y \; \varepsilon \; \text {or} \; \tau = Y \frac{\Delta \ell}{\ell_o} \; \therefore \; \Delta \ell = \frac{\tau \ell_o}{Y} \\ \therefore \; \Delta \ell = \frac{(3.00 \times 10^8 \; \text {N/m}^2)(6.25 \; \text m)}{2.00 \times 10^8 \; \text {N/m}^2}= 9.38\times 10^{-3} \text m = 9.38 \; \text {mm}\)

(c)

\(\begin {align} \text{At breaking,} \; \tau & = (6.60 \times 10^{-3})Y \\ & = (6.60 \times 10^{-3})(2.00 \times 10^{11} \; \text {N/m}^2) \\ & = 1.32 \times 10^9 \; \text {N/ m}^2 \end {align}\)

\(\text {As in part (a),} \; w = \tau A\\ \therefore \; w = (1.32 \times 10^9 \; \text {N/m}^2)(0.0450 \; \text m^2) = 5.94 \times 10^7 \; \text N\)

(a)

\(\tau_s = \frac{F_s}{A}= \frac{0.245 \; \text N}{(40.0 \times 10^{-3} \text m)(40.0 \times 10^{-3} \text m)}= 153 \; \text {N/m}^2 \quad (153._1 \; \text {N/m}^2)\)

(b) \(\varepsilon_s = \frac{\Delta x}{\ell}= \frac{5.50 \; \text {mm}}{20.0 \; \text{mm}}= 0.275\)

(c) \(\tau_s = G\varepsilon_s \; \therefore\; G = \frac{\tau_s}{\varepsilon_s}= \frac{153._1\; \text {N/m}^2}{0.275}= 557\; \text {N/m}^2\)

\(\tau_s = G\; \varepsilon_s \; \text {or} \; \frac{F_s}{A} = G\; \tan \phi \; \therefore \; \phi = \tan ^{-1} \bigg( \frac{F_s}{GA} \bigg) \\ \therefore \; \phi \tan ^{-1} \bigg( \frac{1.50 \times 10^6 \; \text N}{(1.00 \times 10^{10} \text {N/m}^2)(0.300 \; \text m)^2} \bigg) = 0.0955^\circ = 1.67 \times 10^{-3} \text {rad}\)

\(\begin {align} \tau_s & = \frac{\pi r^4 \;G \theta}{2 \ell} = \therefore \; \theta = \frac{2 \ell \tau_s}{\pi r^4 \; G} \\ \therefore \; \theta & = \frac{2(3.50 \; \text m)(170\; \text N \cdot \text m)}{\pi (2.60 \times 10^{-2}\; \text m)^4(8.00 \times 10^{10}\; \text {N/m}^2)}\\ & = 0.0103_6 \; \text{rad} \times \frac{180^\circ}{\pi \; \text{rad}} \\ & = 0.594 ^\circ \end {align}\)

\(\begin {align} \tau_H & = \frac{2 \pi G\; \overline{r}^3 t \theta H}{L_H} \Rightarrow \theta _H = \frac{\tau_H L_H}{2 \pi G\; \overline r ^3 t} \\ \tau_S & = \frac{\pi r^4 G \theta S}{2L_S} \Rightarrow \theta _S = \frac{2\tau_S L_S}{\pi \gamma^4 G} \\ \frac{\theta _H}{\theta _S} & = \frac{\tau_HL_H}{2 \pi G\; \overline r^3 t} \cdot \frac{\pi \gamma^4 G}{2 \tau_SL_S} = \frac{\gamma^4 \tau_HL_H}{4 \overline \gamma^3 t \tau_SL_S} \quad [1] \end {align}\)

\(\begin {align} \text {since}\; \tau_H & = \tau_S, \; L_H = L_S, \\ \overline \gamma &= \frac{\gamma _{inner}+ \gamma _{out}}{1}= \frac{r + 1.2 \gamma}{2} = 1.1 \gamma \\ t & = \gamma _{out} - \gamma _{inner}= 1.2 \gamma - \gamma = 0.2 \gamma \end {align}\)

Substitute into \([1]\)

\(\begin {align} \frac{\theta_H}{\theta_S} & = \frac{\gamma ^4}{4 \overline \gamma ^3 t}= \frac{r^4}{4 \times 1.1^3r^3 \times 0.2\gamma}= 0.939 \\ \frac{\theta _S}{\theta _H} & = 1.06 \end {align}\)

If it takes \(100\; \text g\) of wool to knit a sleeveless sweater for a \(15\; \text {kg}\) child, approximately how much wool is required for a similar sweater for a \(120\; \text {kg}\) man? Assume that all dimensions on the man are simple multiple of those on the child.

You should realize that this is a problem in scaling. In both cases, we have to cover a surface.

 It is important notice that in both sweaters, the thickness of material will be the same. Thus the wool covering one square metre of a child will have the same mass as the wool covering one square metre of a man.

 It should be obvious that:

\(\frac{\text{mass of wool for man}}{\text{area of man}} = \frac{\text{area of man}}{\text{area of child}}\)

We do not need to know the absolute area of either the child or the man; all we need is the ratio. Since the child and the man have the same density, then the ratio of their volumes will be the same as the ratio of their masses.

How many times is the volume of the man than that of the child?

You should have found that:

\(\frac{\text{volume of man}}{\text{volume of child}} = \frac{\text{mass of man}}{\text{mass of child}} = \frac{120}{15}= 8\)

 If the linear dimensions of the man are greater than those of the child by a factor of '\(L\)', then the volume of the man will be greater than the child by a factor of '\(L^3\)'.

 So, \(L^3 = 8.\) This gives us a scaling factor of what? (i.e. \(L = ?\))

Since \(L^3 = 8,\) then \(L = 2.\)

We are now in a position to calculate the ratio of the area of the man relative to that of the child.

Calculate this ratio.

Remember, areas are two dimensional, so scale as L² . Thus the area of the man is 4 times that of the child.

Earlier we wrote down:

\(\frac{\text{mass of wool for man}}{\text{area of man}} = \frac{\text{area of man}}{\text{area of child}}\)

Now calculate the mass of wool needed for the man's sweater.

Because the man has four times the area, it will take four times as much wool to cover him.

Therefore, \(4 \times100\; \text g = 400\; \text g\) of wool needed to cover the man.

\(\frac{mass_{Man}}{mass_{Dog}} = \frac{70.0 \; \text{kg}}{2.50 \; \text{kg}} = L^3 \Rightarrow L = 3.03_7\)

Water on skin is \(\propto\) surface area

\(\begin {align} \therefore \; \frac{water_{Man}}{water_{Dog}} &= L^2 \; \therefore \; water_{Dog} = \frac{water_{Man}}{L^2} \\ \therefore \; water_{Dog} & = \frac{0.330\; \text{kg}}{(3.03_7)^2}= 0.0358\; \text{kg} \quad (0.0357_9\; \text{kg})\\ \frac{water_{Man}}{mass_{Man}} & = \frac{0.0330\; \text{kg}}{70.0\; \text{kg}}\times 100\% = 0.471 \% \\ \frac{water_{Dog}}{mass_{Dog}} &= \frac{0.0357_9\; \text{kg}}{2.50\; \text{kg}} \times 100\% = 1.43\% \end{align}\)

For same thickness, mass \(\propto\) surface area

\(\begin {align} \therefore \; \frac{mass_{large}}{mass_{small}} & = \frac{2Mg}{Mg}= L^2 \; \therefore l = \sqrt{2} \\ \frac{diameter_{large}}{diameter_{small}} &= L \end {align}\)

\(\therefore\; diameter_{large} = (L)(diameter_{small})= \sqrt{2}\;(20.0\; \text{cm}) = 28.3\; \text{cm}\)

\(\text{oxygen requirement:}\; O_{2R} \propto mass \;\propto L^3 \propto r^3 \\ \text{oxygen intake:}\; O_{2i} \propto surface \; area \propto L^2 \propto r^2 \\ \therefore \; \frac{O_{2i}}{O_{2R}} \propto \frac{r^2}{r^3} \propto \frac{1}{r} \quad (\text{or} \propto r^{-1})\)

As \(r\) increases, the ration \(O_{2i}/O_{2R}\) decreases. Eventually, \(O_{2i}\) will become less than \(O_{2R},\) and the cell will be oxygen-starved. Thus, a cell cannot grow indefinitely and survive.

(a)

\(\begin {align} \frac{mass_{Tall}}{mass_{Short}} & = \frac{90.0 \; \text{kg}}{60.0\; \text{kg}}= L^3 \Rightarrow L = \sqrt[3]{1.5} = 1.14_5 \\ \frac{mass_{LiftedTall}}{mass_{LiftedShort}} & = L^2 \; (\text{since muscle force} \propto \text{area})\\ \therefore \; mass_{LS} &= \frac{mass_{LT}}{L^2}= \frac{140\text{kg}}{(1.14_5)^2} = 107 \; \text{kg} \quad (106.8\; \text{kg}) \end {align} \)

(b)

\(\begin {align} \frac{mass_{LT}}{mass_{T}} &= \frac{140\; \text{kg}}{90.0 \; \text{kg}}= 1.56 \\ \frac{mass_{LS}}{mass_S} & = \frac{106._8 \; \text{kg}}{60.0\; \text{kg}}= 1.78 \end {align}\)

\(\frac{height_H}{height_P} = \frac{2.50\; \text{m}}{1.50\; \text{m}}= \frac{5}{3} = L \\ \sum \tau= 0, \text{about 0 (pivot)} \\ \therefore \; (m_Pg)(d_P)- (m_Hg)(d_H)= 0 \\ \therefore\; \frac{d_P}{d_H} = \frac{m_H}{m_P} = L^3 = \bigg( \frac{5}{3} \bigg)^3 = 4.63 \)

If a giant species of ant were developed with all body measurements (excluding legs) 10 times as large as the common ant, what would the diameter of the legs, in order to be relatively as strong as the common ant, have to be?

You first need to find out the factor by which the volume increases. Do this now.

The volume would increase by the cube of the linear dimensions. That is, \(\mathrm{L^3 = 10^3 = 1000.}\) Consequently, the legs would have to be 1000 times as strong as before.

The legs can be considered as pillars (or cylinders), and the strength of a pillar is dependent on its area. To be 1000 times as strong the legs must therefore have 1000 times the area as before.

To achieve this, the diameter of the legs would have to increase by what factor?

The diameter must increase by the same factor as the radius (\(\mathrm{r}\)), and recall that area (\(\mathrm{A}\)) is proportional to the square of the radius; i.e. \(\mathrm{A ^{\alpha}r².}\)

 So, taking the square root of 1000, we find the radius needs to increase by 31.7 times. Therefore, the diameter must also increase by 31.7 times.

Subscript: Elephant, Cat, Skeletal

\(\begin {align} \frac{M_{SE}}{M_{SC}} & = \frac{M_E}{M_C}^{1.08}\\ M_{SC}= 0.070\; M_C & = 0.070 (5.0 \; \text{kg})= 0.35\; \text{kg} \\ \therefore\; \frac{M_{SE}}{0.35} & = \bigg( \frac{7000}{5.0} \bigg)^{1.08} \Rightarrow M_{SE} = 874.8\; \text{kg} \\ \therefore\; \frac{M_{SE}}{M_E} & = \frac{874.8}{7000} \times 100 \% = 12\% \end{align}\)

(a) For each leg, \(\tau = \frac{F}{A}= \frac{(m/4)g}{\pi r^2}\)

\(\therefore \; \tau = \frac{(350\; \text{kg}/4)(9.80\;\text{m/s}^2)}{\pi(5.50 \times 10^{-2}\text m)^2} = 9.02 \times 10^4 \; \text{N/m}^2 \\ (9.02_3 \times 10^4\; \text{N/m}^2)\)

(b) For larger animal, mass \(m_{\ell}\) leg radius \(r_{\ell}\) :

\(\begin {align} \tau = \frac{(m_{\ell}/4)g}{\pi r_{\ell}{^2}} \Rightarrow r_{\ell} & = \sqrt{\frac{m_{\ell}g}{4 \tau \pi}} \\ \therefore \; r_{\ell} = \sqrt{\frac{(600)(9.80)}{4(9.02_3 \times 10^4)\pi}} & = 0.0720\; \text{m} = 7.20\; \text{cm} \end{align}\)

(a)

\(\tau = Y \varepsilon \; \text{or} \; \frac{F}{A} = Y \frac{\Delta \ell}{\ell_o} \\ \begin {align} \text{Given:}\; \frac{\Delta \ell}{\ell _o} &= 1.00 \% = 0.0100 \\ \therefore \; F - YA \frac{\Delta \ell}{\ell_o} & = (1.40\times 10^{10} \text{N/m}^2)(2.90 \times 10^{-4} \text{m}^2)(0.0100) \\ & = 4.06 \times 10^4 \text N \end {align}\)

(b) Determine the acceleration corresponding to given (normal) force during loading:

\(\sum F_y = m\; a_y \therefore mg - \text N = m\;a_y = g - \frac{\text N}{\text m} \\ \therefore a_y = 9.80\; \text{m/s}^2 - \frac{4.06 \times 10^4 \; \text N}{(75.0\; \text{kg})/2}= -1073\; \text{m/s}^2\)

Determine downward velocity just before landing:

\(v_{oy} = ?, \; v_y = 0, \; a_y = -1073\; \text{m/s}^2, \; t = 0.0310 \; \text s \\ v_y = v_{oy} + a_y t \Rightarrow v_{oy} = 33.26\; \text{m/s}\)

Use conservation of energy to determine height:

\(\text{initial}\;PE_{grav} = KE\; \text{just before landing} \\ \therefore\; m\; g\; h = \frac{1}{2}mv^2 (\text{where} v = 33.26\;\text{m/s}) \\ \therefore\; h = \frac{v^2}{29} \Rightarrow h = 56.4\; \text m\)

(a) 

\(\text{Stresses:} \; \tau_A = \tau_B \; \therefore \; \frac{F_B}{A_A} = \frac{F_B}{A_B} \; \therefore \; \frac{F_B}{F_A} = \frac{A_B}{A_A} \\ \text{But} \; \frac{A_B}{A_A} = \frac{2.00}{1.00} = 2.00 \; \therefore \frac{F_B}{F_A} = 2.00\\ \text{i.e., } \; \frac{T_B}{T_A} = 2.00\; \text{or} \; T_B = 2.00\; T_A \quad (T = tension)\)

\(\sum F_y = m\; a_y = 0 \; \therefore \; T_A + T_B -mg-mg = 0 \therefore \; T_A + T_B = 2mg\\ \text {But}\; T_B = 2T_A\; \therefore \; T_A+2T_A = 2mg \; \therefore \; T-A = \frac{2}{3}mg \; \text{and} \; T_B = 2T_A =\frac{4}{3} mg \\ \sum \tau = 0, \text{about P} \therefore (T_A)(0)-mg \frac{\ell}{2}-mgx +T_B \ell = 0 \\ \text{But} \; T_B = \frac{4}{3}mg \; \therefore\; -mg \frac{\ell }{2}-mgx+\frac{4}{3}mg \ell = 0 \Rightarrow x = \frac{5}{6} \ell\)

(b)

\(\frac{F}{A} = Y \varepsilon \; \therefore\; \varepsilon = \frac{F}{A_y} \; \therefore \; \text{same strain} \; \varepsilon \Rightarrow \frac{F_A}{A_AY_A} = \frac{F_B}{A_BY_B} \\ \therefore \; \frac{F_B}{F_A}= \frac{A_BY_B}{A_AY_A} = \bigg( \frac{2.00}{1.00} \bigg) \bigg( \frac{1.60}{2.40} \bigg) = \frac{4}{3}\; \therefore \; T_B = \frac{4}{3} T_A\)

Using same FBD as in (a):

\(\sum F_y= 0\Rightarrow T_A+T_B = 2mg, \text{as in (a)} \\ T_B = \frac{4}{3} T_A \; \therefore \; T_A + \frac{4}{3}T_A = 2mg \; \therefore \; T_A = \frac{6}{7} mg \; \text{and}\;T_B = \frac{4}{3}T_A = \frac{8}{7} mg\\ \sum \tau = 0, \text{about P} \Rightarrow -mg \frac{\ell}{2}-mgx+T_B \ell = 0, \text{as in (a)} \\ T_B = \frac{8}{7}mg \Rightarrow -mg \frac{\ell}{2}- mgx+\frac{8}{7}mg \ell = 0 \Rightarrow x = \frac{9}{14} \ell\)

Max. static friction \(F_{Max}= \mu_s \text N\)

\(\sum F_y = ma_y = 0 \quad \uparrow+y \\ \therefore \text N - mg = 0\therefore \; \text N = mg \\ \therefore F_{max} = \mu_s \text N = \mu_s mg\)

On verge of slipping, \(\sum F_x = ma_x = 0\) and friction is max.

\(\therefore\; F_s - F_{max}= 0 \\ \begin {align} \therefore \; F_s & = F_{max} = \mu_s mg \\ \therefore\; F_S & = 0.880 (0.450 \text {kg})(9.80\; \text{m/s}^2)\\ &= 3.88_1 \; \text N \end {align}\)

(a) \(\tau_s = \frac{F_s}{A} = \frac{3.88_1 \text N}{(8.00 \times 10 ^{-2}\text m)^2}= 606\; \text{N/m}^2 \quad (606._4 \; \text{N/m}^2)\)

(b) \(\tau_s = G \varepsilon_s \therefore \varepsilon_s = \frac{\tau_s}{G} = \frac{606._4\; \text{N/m}^2}{1.60 \times 10^7 \; \text{N/m}^2}= 3.79\times 10 ^{-5} \quad(3.79_0 \times 10^{-5})\)

(c) \(\varepsilon_s = \frac{\Delta x}{s}\; \therefore \Delta x = \varepsilon_s \ell = (3.79_o \times 10^{-5})(2.00 \times 10^{-2} \text m) = 7.58 \times 10^{-7} \text m\)

(a)

\(\begin {align} \text {tensile force} & = \text{vertical component of } \overrightarrow F \\ & = (2.50 \times 10^3 \text N) \sin 30.0 ^\circ \\ &= 1.25 \times 10^3 \text N \end {align}\)

\(\frac{F}{A} = Y \frac{\Delta \ell}{\ell _o} \therefore \Delta \ell = \frac{F \ell_o }{AY}\)

\(\begin {align} \therefore \Delta \ell & = \frac{(1.25 \times 10^3 \text N)(1.00 \times 10^{-2} \text m)}{(1.00 \times 10^{-2}\text m)(1.80 \times 10^{-2} \text m)(1.40 \times 10^{10} \; \text{N/m}^2)} \\ &= 4.96 \times 10 ^{-6} \text m \quad (= 4.96 \times 10^{-4}\text m) \end {align}\)

(b)

\(\begin {align} \text {shear force}\; F_s & = \text{horizontal component of}\; \overrightarrow F \\ &= (2.50 \times 10^3\; \text N) \cos 30.0^\circ \\ & = 2165\; \text N \end {align}\)

\(\frac{F_s}{A}= G \frac{\Delta x}{\ell} \; \therefore \; \Delta x = \frac{F_s \ell}{A G}\)

\(\begin {align} \therefore \; \Delta x & = \frac{(2165\; \text N)(1.00 \times 10^{-2}\text m)}{(1.00 \times 10^{-2} \;\text m)(1.80\times 10^{-2}\; \text m)(9.00 \times 10^9\; \text{N/m}^2)} \\ & = 1.34 \times 10^{-5} \; \text m \quad (= 1.34 \times 10^{-3} \; \text{cm}) \end {align}\)

(a)

\(\text {volume of cylinder} = \pi r^2 h \\ \text{volume of hemisphere} = \frac{1}{2}\bigg( \frac{4}{3}\pi r^3 \bigg) = \frac{2}{3} \pi r^3 \\ \therefore \; \text{total volume} = \pi r^2h + \frac{2}{3}\pi r^3 \\ \text{area of cylinder} = \text{circumference} \times \text{height} \\ = 2 \pi rh \\ \text {area of hemisphere} = \frac{1}{2}(4 \pi r^2) = 2\pi r^2 \\ \therefore \text{total area} = 2 \pi rh + 2 \pi r^2\)

(b) \(\text {Let}\; \frac{h}{r} = c \;(constant) \; \therefore \; h = cr\)

\(\begin {align} \text{From (a), volume} \; V & = \pi r^2 h + \frac{2}{3} \pi r^3 \\ &= \pi r^2 (cr) +\frac{2}{3} \pi r^3 \\ &= \bigg( \pi c + \frac{2}{3} \pi \bigg) r^3 \\ & = D\;r^3, \text{where} \; D = \pi c+ \frac{2}{3} \pi = \text{const.} \end {align}\)

\(\begin {align} \text{Initial volume} \; V_1 & = D\; r_1{^3} \\ \text{New volume}\; \underbrace{ V_2} & = 2V_1 \\ \therefore \; D\; r_2{^3} & = 2Dr_1 {^3} \Rightarrow r_2 = \sqrt[3] {2}\; r_1 \end{align}\)

\(\text{Then,} \; h_2 = cr_2 = c \sqrt[3] {2}\; r_1 = \sqrt[3]{2} \; (cr_1 ) = \sqrt[3]{2} \; h_1\)

\(\begin {align} \text{New area} \; A_2 & = 2\pi r_2h_2 + 2 \pi r_2{^2} \\ &= 2\pi \bigg( \sqrt[3]{2} \; r_1\bigg) \bigg( \sqrt [3]{2}\; h_1 \bigg) + 2\pi \bigg( \sqrt [3] {2}\; r_1 \bigg)^2 \\ &= \bigg( \sqrt[3]{2} \bigg)^2 [2\pi r_1h_1 + 2\pi r_1{^2}]\\ &= 2^{2/3} A_1 \end {align}\)

(c)

\(\text{Volume}\; V = \pi r^2 h + \frac{2}{3}\pi r^3 \\ \text{Initial}\; V_1 = \pi r_1{^2}h_1 + \frac{2}{3}\pi r_1{^3}\)

Radius remins constant at \(r_1\)

\(\therefore\; \text {New} \; V_2 = \pi r_1{^2}h_1+\frac{2}{3}\pi r_2{^3}\\ \text{But} \; V_2 = 2V_1 \\ \)

\(\begin {align} \therefore\; \pi r_1 {^2}h_2 + \frac{2}{3} \pi r_2{^3} & = 2 \bigg( \pi r_1{^2}h_1+ \frac{2}{3} \pi r_1{^3} \bigg) \\ & = 2\pi r_1{^2h_1 + \frac{4}{3}\pi r_1{^3}} \\ \therefore\pi r_1{^2}h_2 &= 2\pi r_1{^2} h_1 + \frac{2}{3}\pi r_1{^3} \\ \therefore h_2 &= 2h_1 + \frac{2}{3} r_1 \end {align}\)

\(\begin {align} \text{New area} \; A_2 & = 2\pi r_1h_2 + 2\pi r_1{^2}\\ &= 2\pi r_1 \bigg( 2h_1 + \frac{2}{3} r_1 \bigg) + 2 \pi r_1{^2}\\ & = 4\pi r_1 h_1 + \frac{4 \pi}{3}r_1{^2} + 2 \pi r_1{^2} \\ & = 4\pi r_1h_1 +\frac{10 \pi}{3}r_1{^2} \end {align}\)

Rewrite this in terms of:

\(\begin {align} 2A_1 & = 2 (2\pi r_1h_1 + 2\pi r_1{^2})\\ & = 4 \pi r_1 h_1 + 4 \pi r_1{^2} \end {align}\)

\(\therefore A_2 = \underbrace {4\pi r_1h_1+ 4 \pi r_1{^2}}_{2A_1} - \underbrace{4\pi r_1{^2}+ \frac{10 \pi}{3} r_1{^2}}_{- \frac{2 \pi}{3}r_1{^2}} \\ \therefore A_2 = 2A_1 - \frac{2 \pi}{3}r_1{^2}\)

Normal pig:

\(\text {mass} \; m_1 \quad 4\; \text{legs} \\ \text{Stress in each leg} = \frac{mg/4}{A} = \frac{mg/4}{\pi r^2} \quad [1]\)

Super pig:

\(\require {enclose} L = 2 \Rightarrow \text{mass} \; 8\; \text{m}\quad (\text{mass}\; \propto \; L^3) \\ \enclose{verticalstrike}{\varepsilon} \text{leg radius} \; 2r \\ \enclose{verticalstrike}{\varepsilon}\; n \; \text{legs} \\ \text{Stress in each leg} = \frac{8mg/n}{\pi (2r)^2} \quad [2]\)

\(\begin {align} \text{Stress in }\; [1] & = \text{Stress in}\; [2] \\ \therefore \frac{mg/4}{\pi r^2} & = \frac{8mg/n}{\pi (2r)^2} \end {align} \\ \text{Solving for} \; n \Rightarrow n = 8, \text{i.e., 4 extra legs}\)

Egg masses: \(\frac{m_{large}}{m_{small}} \dot = L^3 \)

\(\therefore \frac{300\; \text g}{60.0\; \text g} = L^3 \Rightarrow L = \sqrt[3]{5.00}\)

Shell mass: \(m_{shell} \propto \underbrace{\text{surface area}}_{A} \times \underbrace{thickness}_{t}\)

\(\begin {align} \therefore \frac{m_{sh,l}}{m_{sh,s}} & = \frac{A_l}{A_s}\frac{t_l}{t_s} \quad [1]\\ \text {But}\;\frac{A_l}{A_s} & = L^2 \\ \therefore \; [1] \Rightarrow \frac{7.60 \; \text g}{2.00 \; \text g} & = \bigg( \sqrt[3]{5.00} \bigg)^2 \frac{t_l}{t_s} \\ \Rightarrow \frac{t_l}{t_s} & = 1.30 \end {align}\)