Biophysics Textbook Questions - Chapter 8

What horizontal force will stop, in \(\mathrm{4\; seconds,}\) a \(\mathrm{5\; kg}\) mass sliding on a frictionless floor if the mass has an initial speed of \(\mathrm{12\; m\; s}\) ?

If you knew the acceleration then this should be a simple exercise of applying Newton's second law \(\mathrm{(F=ma)}\).

To find the acceleration you will have to use one of the kinematic equations, each of which uses 4 of the variables. (ie: initial velocity, final velocity, distance, time, and acceleration)

List the three variables given and the one you wish to find.

Your list of known values should be:

\(\mathrm{    initial \;velocity   \quad  u = 15 \;m/s \\     final \;velocity    \quad    v = 0 \;m/s \\     time    \quad        t = 4 \;s}\)
 
You wish to find acceleration '\(\mathrm{a}\)'.

Write down the equation you would use to solve for '\(\mathrm{a.}\)'

Since your know variables are:

\(\mathrm{    initial \;velocity  \quad u = 15 \;m/s \\     final \;velocity    \quad    v = 0 \;m/s \\     time      \quad      t = 4 \;s}\)

You should be using the formula

\(\mathrm{v = u + at}\)
 
Now solve for the acceleration \(\mathrm{a.}\)

Substitution into \(\mathrm{v = u + at}\) should give:

\(\mathrm{        v =   u        +    at \\         0 = 15\; m/s  +  a \times 4 \;s}\)

solve this to get:

\(\mathrm{a = -3 \;m/s^2}\)

So the magnitude of the acceleration is \(\mathrm{3.}\)

Substitute into Newton's second law to find the force required to stop the mass.

The correct answer is \(\mathrm{15\; N.}\)

 Remember to specify the magnitude \(\mathrm{(15)}\) as well as the units \(\mathrm{(N).}\)

\(\mathrm{\sum F = ma \\ \therefore F = (78.0)(14.0)\\ = 1.09 \times 10^3\;N}\)

The acceleration of any object is caused by forces exerted by objects that are exrernal to the accelerating object. The force that accelerates the runner is exerted by the blocks. (The runner exerts a force on the blocks; by Newton's 3rd law, the blocks exert an equal and opposite force on the runner.)

(a) First, find acceleration:

\(\mathrm{x = x_o + v_o t +\frac{1}{2} a\; t^2 \\ where\; x_o = 0,\; and\; v_o = 0}\)

\(\mathrm{\therefore 11.5 = \frac{1}{2}\;a\;(4.50)^2\\ \therefore a = 1.13_6\;m/s^2}\)

\(\mathrm{\sum F = ma \\ \therefore 85.0 = m (1.13_6)\\ \therefore m = 74.8\; kg}\)

(b) After first \(\mathrm{4.50\;s,}\)
\(\mathrm{v = v_o +at\\ = 0+(1.13_6)(4.50)\\ = 5.11_2\;m/s}\)

After the person stops pushing, 

\(\mathrm{\sum F = 0\\ \therefore a = 0\\ \therefore v = constant}\)

\(\mathrm{\therefore\; distance = v \cdot \Delta t\\ = (5.11_2)(4.50)\\ = 23.0\;m}\)

(a)

\(\mathrm{\uparrow + \\ v= v_o+at\\ \therefore 0=-12+a(3.0 \times 10^{-3})\\ \therefore a = + \;4.0 \times 10^{-3} \;m/s^2 (note \; that + \; is \; up)\\ \therefore a \; is\; 4.0 \times 10^{3}\; m/s^2 \; upward}\)

(b)

\(\mathrm{\sum F = ma \\ = (0.66)(4.0\times 10^3)\\ = + 2.6 \times 10^3\; N}\)

\(\therefore\) the force is \(\mathrm{2.6 \times 10^3 \; N }\) upward, exerted by the brick on the hand

Forces on parachutist:

\(\mathrm{\sum F = ma \\ \therefore m\;g - F_{parachute}= ma \\ \therefore (61.0)(9.80)- 342 = (61.0)a \\ \therefore a = +\;4.19\; m/s^2\\ \therefore a \; is \; 4.19\;m/s^2 \; downward}\)

(a)

\(\mathrm{F_G = mg \\ \therefore m = \frac{F_G}{g}= \frac{590\; N}{9.80\;m/s^2}= 60.2\;kg\quad (60.2_o\;kg)}\)

(b)

On Mars, \(\mathrm{m = 60.2\; kg}\)

but \(\mathrm{F_G = mg = (60.2\; kg)(3.72\;m/s^2)= 224\;N}\)

\(\mathrm{g = \frac{GM}{r^2} \\ = \frac{(6.673 \times 10^{-11}N \cdot m^2/kg^2)(7.00 \times 10^{10} kg)}{(175 \times 10^3m)^2} \\ = 1.52_5 \times 10^{-10}\;m/s^2}\)

\(\mathrm{F_G = mg \\ = (80.0\; kg)(1.52_5 \times 10^{-10}\;m/s^2) \\ = 1.22 \times 10^{-8}N}\)

Forces acting on a crow:

\(\mathrm{\sum F_y = ma_y = 0\\ \therefore T_y + T_y- mg = 0 \\ \therefore T_y = \frac{mg}{2}}\)

Now, 

\(\mathrm{T_y = T \sin \theta \\ \therefore T = \frac{mg}{2 \sin \theta} \quad [1]}\)

Determine \(\theta :\)

\(\mathrm{\theta = \tan^{-1} \bigg( \frac{0.098}{25.0} \bigg)= 0.22_5 {^\circ}\\ Subst\cdot in \quad [1] \\ \therefore T = \frac{(1.10 \; kg)(9.80\;m/s^2)}{2 \sin(0.22_5{^\circ})}\\ = 1.4 \times 10^3\;N }\)

\(\mathrm{w = mg = (8.50\;kg)(9.80\;m/s^2)= 83.3\;N}\)

\(\mathrm{ \overrightarrow v = const.\\ \therefore \sum \overrightarrow F = 0\\ \therefore \sum F_y = 0 \\ \therefore F_{up-mg}= 0 \\ \therefore F_{up}= mg = 83.3\; N}\)

(a)

\(\mathrm{\sum F_x = 0\\ \therefore T_x - F_{wind}= 0\\ \therefore F_{wind}= T_x = T\sin \theta = (2.00 \times 10^3 \; N)\sin 20.0^\circ \\ = 684\;N}\)

(b)

\(\mathrm{\sum F_y = 0 \\ \therefore F_{buoyant} - T \cos \theta = 0 \\ \therefore F_{buoyant}= (2.00 \times 10^3 \;N) \cos 20.0^\circ = 1.88 \times 10^3 \;N}\)

(a) Forces on a "box":

\(\mathrm{\sum F_y = 0 \therefore T_c = w}\)

\(\mathrm{\sum F_x = 0\\ \therefore T_B \cos 47^\circ - T_A \cos 32^\circ = 0\\ \therefore T_B = 1.2_4 \; T_A}\)

\(\mathrm{\sum F_y = 0 \\ \therefore T_A \sin 32^\circ + T_B \sin 47^\circ = T_C = 0}\)

\(\mathrm{Subst. \; T_C = w, and \; T_B = 1.2_4\; T_A \\ \therefore T_A = \sin 32^\circ + (1.2_4 T_A) \sin 47^\circ - w = 0 \\ \therefore T-A = 0.69 \; w \quad (0.69_5 w)}\)

Then,  \(\mathrm{T_B = 1.2_4 T_A = 0.86\; w}\)

(b) As in part (a), T_C = w

Then, Forces on the knot:

\(\mathrm{\sum F_x = 0\\ \therefore T_B \cos 47^\circ - T_A \sin 80^\circ = 0 \\ \therefore T_B = 1.4_4 \; T_A}\)

\(\mathrm{\sum F_y = 0 \\ \therefore T_B \sin 47^\circ - T_A \cos 80^\circ - T_C = 0}\)

\(\mathrm{Subst. T_B = 1.4_4 \;T_A \; and\; T_C = w \\ \therefore (1.4_4 \; T_A)\sin 47^\circ - T_A \cos 80^\circ - w = 0 \\ \therefore T_A = 1.1\;w \quad (1.1_3 \; w)}\)

Then,  \(\mathrm{T_B = 1.4_4 \;T_A = 1.6\;w}\)

Forces acting on a wagon.

\(\mathrm{\overrightarrow v = const. \\ \therefore \overrightarrow a = 0 \\ \therefore \sum F_x = ma_x = 0 \\ \therefore F - mg \sin \theta = 0 \\ \therefore F = mg \sin 35.9 ^\circ \\ (200\; N) \sin 35.9 ^\circ \\ = 117\; N}\)

Forces on a student

\(\mathrm{\uparrow +y \\ \sum F_y = m\;a_y \\ \therefore F_{scale} -m\;g = m\; a_y \\ \therefore 550 - (66.0)(9.80)= 66.0 a_y \\ \therefore a_y = -1.47\;m/s^2}\)

\(\therefore\) the acceleration is \(\mathrm{1.47\;m/s^2}\) downward

Ice on an incline:

\(\mathrm{x = x_o + v_{ox}t + \frac{1}{2}\; a_x \; t^2 \\ \therefore 5.00 = 0+0+\frac{1}{2}\; a_x (1.68)^2 \\ \therefore a_x = 3.54_3\; m/s^2}\)

Forces acting on ice:

\(\mathrm{\sum F_x = ma_x\\ \therefore m\;g \sin \theta = ma_x\\ \therefore \sin^{-1}\bigg( \frac{a_x}{g} \bigg)= \sin ^{-1} \bigg(\frac{3.54_3}{9.80}\bigg) = 21.2^\circ}\)

Forces acting ona cutter:

\(\mathrm{\overrightarrow v = const.\quad \therefore \overrightarrow a = 0 \\ \therefore \sum F_x = m\;a_x = 0 \\ \therefore F_{Horse}- F_f = 0 \\Subst. \; F_f = \mu _k N\quad \therefore F_{Horse}= \mu_KN}\)

Determine N from:

\(\mathrm{ \underbrace {\sum F_y = m\; a_y = 0} \\N- mg= 0\; \therefore N = mg \\ \therefore F_{Horse}= \mu _K mg = 0.110 (250\; kg)(9.80 m/s^2 )= 2.70 \times 10^2 \; N}\)

Forces acting on skier:
( \(\theta\) = angle between hill and horizontal)

\(\mathrm{\overrightarrow v = constant\; \therefore \; \overrightarrow a = 0\\ \therefore \sum F_x = m\; a_x = 0 \\ \therefore \; m\; g \sin \theta - F_f= 0 \\ F_f = \mu _K N\; \therefore m\; g \sin \theta - \mu _K \;N= 0 \\ \therefore \mu _K = \frac{m\;g \sin \theta}{N}}\)

Determine N from:

\(\mathrm{\underbrace{\sum F_y = m\; a_y = 0}\\ N-m\; g \cos \theta = 0 \\ \therefore N = m\; g \cos \theta \\ \therefore \mu_K = \frac{m\;g \sin \theta}{m\;g \cos \theta}= \tan \theta = \tan 20.0^\circ = 0.364}\)

Force diagram is the same as that for Exercise 8-16, with \(\mathrm{\overrightarrow {F_f}}\) replaced by \(\mathrm{\overrightarrow F_{Max}}\) , where \(\mathrm{F_{Max}= \mu_s\; N.}\)

If the skier starts moving without pushing, 

\(\mathrm{\sum F_x = m\; a_x > 0\\ \therefore \;m\; g \; \sin \theta - F_{Max}>0}\)

But \(\mathrm{ F_{Max}= \mu _s\; N}\)

and, as in Exercise 8-16, \(\mathrm{N = m\;g \cos \theta}\)

\(\mathrm{\therefore \;m\;g\; \sin \theta - \mu_s m\; g\; \cos \theta > 0 \\ \therefore \sin \theta > \mu_s \cos \theta \\ \therefore \tan \theta > \mu_s \; or\; \mu_s < \tan \theta \\ \therefore \mu_s < \tan 15.0^\circ \\ \therefore \mu _s < 0.268}\)

This is very similar to Exercise 8-16, except that  \(\mathrm{a_x \neq 0.}\) The force diagram is identical to that of Exercise 8-16. Determine \(\mathrm{a_x}\) from the given displacement and time:

\(\mathrm{x = x+o +v_{ox}t + \frac{1}{2}a_x t^2 \\ \therefore 11.5 = 0+0 +\frac{1}{2} a_x (2.50)^2 \\ \therefore a_x = 3.68\; m/s^2}\)

Then, as in Exercise 8-16:

\(\mathrm{\sum F_x = m\;a_x \\ m\; g\; \sin \theta - \mu_K m\; g \cos \theta = m\; a_x \\ \therefore \mu _K= \frac{g \sin \theta -a_x}{g \cos \theta}\\ = \frac{9.80 \sin 29.0^\circ -3.68}{9.80 \cos 29.0^\circ} \\ = 0.125}\)

Linear momentum is conserved.

\(\mathrm{\therefore m_1 v_{1x} + m_2v_{2x}= (m_1 +m_2)v_x{'} \\ \therefore 40/0 (2.00)+ 125(-1.50*) = (165)v_x{'} \\ \therefore v_x{'}= -0.652 \;m/s}\)

\(\mathrm{* \;note - in -1.50}\)

\(\mathrm{\therefore}\) the final speed is \(\mathrm{0.625\;m/s}\) and the cars move in the original direction of motion of car two. 

 A \(\mathrm{1\; kg}\) duck is flying horizontally at \(\mathrm{20 \;m\; s}\) when seized by a \(\mathrm{0.8 \;kg}\) hawk diving down at \(\mathrm{30\; m\; s.}\) The hawk is coming in from behind and makes an angle of \(\mathrm{30^\circ}\) from the vertical just before contact. What is the velocity of the birds just after contact?

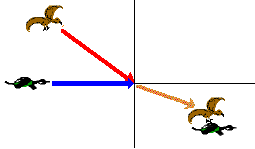
I hope you recognize that this is a problem on conservation of momentum in two dimensions.

Let's first begin by labelling all the known angles and velocities.

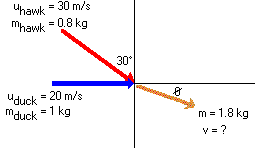
You will have to establish an equation for conservation of momentum in each of the vertical and horizontal directions.

Before you can do this you must represent all velocities by their vertical and horizontal components.

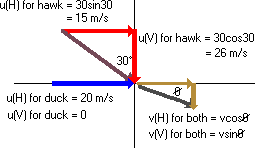
Now you are ready to write down an equation for conservation of momentum in each of the two directions.

 Remember, in each equation the momentum before the collision must equal the momentum after the collision (in that direction).

 Write out the eqautions now.

In the horizontal (or x) direction:

\(\mathrm{Total\; 'x'\; momentum\; before = Total\; 'x'\; momentum\; after \\ m_{duck}\cdot u_{duck\; x-comp}+ m_{hawk}\cdot u_{hawk\; x-comp} = \bigg( m_{duck} + m_{hawk}\bigg)\cdot v_{both\; x-comp}\\ (1\; kg \times 20\; m/s)+(0.8\; kg \times 15\; m/s)= (1.8\; kg \times \cos \theta)\\ 32\; kg \; m/s = (1.8\;kg \times \cos \theta)}\)

And in the vertical (or y) direction:

\(\mathrm{Total\;'y'\; momentum\; before = Total\; 'y' \; momentum\; after\\ m_{hawk}\cdot u_{hawk\; y-comp}= \bigg(m_{duck}+ m_{hawk}\bigg)\cdot v_{both\; y-comp}\\ (0.8\; kg \times 26\; m/s)= (1.8\; kg \times v \sin \theta)}\)

So we now have two equations with two unknowns.

From te x direction: \(\mathrm{32\;kg\;m/s = (1.8\;kg \times v \cos \theta)}\)

From the y direction: \(\mathrm{(0.8\;kg \times 26 \;m/s)= (1.8\;kg \times \sin \theta)}\)

All that is left is to solve for '\(\mathrm{v}\)' and '\(\theta\)'. (First, find \(\theta\), then \(\mathrm{v}\))

The answer is \(\mathrm{\theta = 33^\circ}\) and \(\mathrm{v = 21\; m/s.}\)

The calculation of \(\theta\) was obtained by dividing one equation by the other to get \(\mathrm{\tan\theta = 0.65}\). Once \(\theta\) was determined, \(\mathrm{v}\) is found by substituting \(\theta\) into one of the original equations.

Linear momentum is conserved. 

\(\mathrm{\therefore\; {\underbrace {m_Hv_{Hx}+ m_B v_{Bx} }_\text {before collision}}= \underbrace {(m_H+m_B) v_x{'}}_ \text {after collision} \\ \therefore100(0) + (90.0)(-15.0 \sin 30.0^\circ)= 190\; v_x^{'}\\ note \; negative\; sign \\ \therefore v_x{^{'}} = -3.55_3\; m/s}\)

and

\(\mathrm{m_H v_{Hy}+ m_Bv_{By}= (m_H + m_B)v_y{'}\\ \therefore (100)(10.0)+ (90.0)(-15.0 \cos 30.0^\circ)= 190 \; v_y{'}\\ \therefore v_y{'} = -0.890_1 \;m/s}\)

\(\mathrm{v' = \sqrt {(3.55_3)^2 + (0.890_1)^2}= 3.66\;m/s \\ \theta = \tan ^{-1} \bigg( \frac{0.890_1}{3.55_3} \bigg)= 14.1 ^\circ}\)

Linear momentum is conserved.

\(\mathrm{\therefore m\;v_x = m_1 v_{1x}{'}+m_2v_{2x}{'}\\ \therefore (80.0)(10.0)= 75.0 v_{1x}{'}+ (5.00)(-5.00)\\ \therefore v_{1x}{'}= 11.0\;m/s}\)

(a)

Linear momentum is conserved.

\(\mathrm{\therefore m_1v_{1x}+ m_2v_{2x}= (m+m_2)v_x{'}\\ \therefore (0.400)(13.0)+(70.0)(0)= 70.4\;v_x{'}\\ \therefore v_x{'}= 0.00739\;m/s}\)

(b)

\(\mathrm{m_1v_{1x}+m_2v_{2x}= m_1v_{1x}{'}+m_2v_{2x}{'}\\ \therefore (0.400)(13.0)+(70.0)(0)= (0.400)(-7.50)+(70.0)v_{2x}{'}\\ \therefore v_{2x}{'}= 0.117\;m/s}\)

The work done by the girl goes into grav. P.E. of the toboggan:

\(\mathrm{m\;g\;\Delta y\\ = (4.90\;kg)(9.80\;m/s^2)(28.0\;m)\\ = 1.34 \times 10^3 \;J}\)

(a) Work energy theorem: total work done by all the forces equals change in \(\mathrm{KE.}\)

\(\mathrm{W_{TOT}= \Delta KE}\)

\(\mathrm{\sum F_y = m\;a_y = 0\\ \therefore N = m\;g \\ \therefore F_K = \mu_K \;N = \mu_K\; m\;g}\)

\(\mathrm{W_{TOT}= \Delta KE}\)

\(\mathrm{\therefore \;N \Delta r\; \underbrace {\cos 90^\circ}_\text 0 \;+ m\;g\; \Delta r\; \underbrace {\cos 90^\circ} _\text 0 \; + \mu _K \;m \; g\; \Delta r\; \underbrace {\cos 180^\circ}_ \text {-1} = \frac{1}{2}m (v^2- v_o{^2})\\ where\; v^2 = 0 \\ Solve\; for \; \Delta r \Rightarrow \Delta r = \frac{v_o{^2}}{2g\;\mu_K}\quad [1]}\)

(b) \(\mathrm{\Delta r \propto v_o{^2} \quad (from\; [1])}\)

For \(\mathrm{v_o = 90.0 \;km/h, \Delta r = 89.5 \;m. }\)

\(\mathrm{\therefore \; for\; v_o = 60.0 \; km/h, \Delta r\; can \; be\; determined \\ from= \frac{\Delta r}{89.5\;m}= \frac{(60.0\; km/h)^2}{(90.0\; km/h)^2}\\ \therefore\; \Delta r = 39.8\;m}\)

\(\mathrm{AB = \ell\cos \theta \\ AC = \ell \cos \emptyset}\)

\(\therefore\) at E, the ball is a vertical height of \(\mathrm{\ell (\cos \emptyset -\cos \theta)}\) lower than at D. 

Energy is conserved.

\(\mathrm{\therefore\; KE_D + U_D = KE_E+U_E}\)

Choose \(\mathrm{y = 0}\) at \(\mathrm{E \;\cdot \therefore U_E = 0}\)

\(\mathrm{\therefore \frac{1}{2} m\; v_D{^2} + m\;g [\ell ( \cos \emptyset -\cos \theta]= \frac{1}{2}m\; v_E {^2}\\ where \; v_D = 0 \\ \therefore v_E = \sqrt{2\;g\;\ell(\cos \emptyset - \cos \theta)}\\ = \sqrt{2(9.80)(1.85)(\cos 30.0^\circ - \cos 45.00)}\\ = 2.40\; m/s}\)

\(\mathrm{U = m\; g\; y \\ \therefore 2.00 \times 10^{13}= m(9.80)(250)\\ \therefore m = 8.16 \times 10^9 \; kg}\)

(a) Thermal energy 

\(\begin{align} \mathrm{E_{th}} &= \mathrm{|work\;done\;by\;friction|} \\ & = \mathrm{|W_{f_K}|} \end{align}\)

\(\begin{align} \mathrm{W_{FK}} &= \mathrm{\Delta r\; \underbrace {\cos 180^\circ} _\text {-1}} \\ &= \mathrm{ - F_K \Delta r} \end{align}\)

\(\mathrm{\therefore E _{th}= F_K \Delta r = (7.45 \times 10^3 N)(49.0\;m)= 3.65 \times 10^5 \; J \quad (3.65 \times 10^5 \;J)}\)

(b) The thermal energy produced was originally \(\mathrm{KE}\) of the car. 

\(\mathrm{\therefore KE = \frac{1}{2}m\;v^2 = 3.65_o \times 10^5 \; J \\ v= 87.0\frac{km}{h}\times \frac{1h}{3600s}\times \frac{1000m}{1km}= 24.1_7 \; m/s\\ \Rightarrow m = 1.25 \times 10^3 \; kg}\)

\(\mathrm{P = \frac{E}{t} \therefore t = \frac{E}{P}= \frac{4.00 \times 10^5 \; J}{3.10 \times 10^2 \; W}= 1290\; s= 21.5\; min.}\)

\(\mathrm{P = \frac{E}{t}= \frac{m\; g\; y}{t}= \frac{(65.0)(9.80)(0.360)}{0.840}= 273\; W}\)

\(\mathrm{ Grav. P. E. \;gained = U = m\; g\; y\\ 75.0\% \; of \;this \; grav.P.E. \; comes \; from \; elastic\; P.E.}\) 

\(\begin{align} \mathrm{\therefore Elastic\; P.E.} &= \mathrm{0.750 \;m\;g\;y} \\ & = \mathrm{0.750 (2.15 \times 10^{-7})(9.80)(0.0670)} \\ & = \mathrm{1.06 \times 10^{-7} J} \end{align}\)

\(\mathrm{1.0\;kcal \times \frac{4186\;J}{kcal}= 4186\; J}\)

\(\begin {align} \mathrm{Efficiency = 25\%\; \therefore}\; \mathrm{useful \;energy} &= \mathrm{0.25 (4186\;J)} \\ &= 1.05 \times 10^3 \;J \end {align}\)

Let \(\mathrm{n}\) = number of pushups

\(\mathrm{\therefore \; n\;m\;g\;y= 1.05 \times 10^ \; J \\ n(59\;kg)(9.80\;m/s^2)(0.26\;m)= 1.05 \times 10^3 \; J\\ \therefore \; n = 6.00\\ \therefore \; at\; least\; 7 \; pushups\; are \; needed.}\)

First, determine velocity when jumper leaves the ground. 

\(\mathrm{v_y{^2}= v_{oy}{^2}+ 2a_y (y-y_o)\\ \therefore \; o^2 = v_{oy}{^2}+ 2(-9.80)(1.15)\\ \therefore \; v_{oy}= 4.74_8\; m/s}\)

This velocity of \(\mathrm{4.74_8\; m/s}\) is the final velocity of the ground-contact phase of the jump. 

Consider this phase now. 

\(\mathrm{v_y=4.74_8\; m/s\\ v_{oy}= 0\;m/s \\ t = 0.290 \;s}\)

\(\mathrm{Use\; v_y = v_{oy}+ a_y t \\ \Rightarrow \; a_y = 16.3_7 \; m/s^2}\)

FBD for jumper:

\(\mathrm{\sum F_y = m\;a_y \\ \therefore F_{Ground}- m\;g = m\;a_y \\ \therefore F_{Ground}= m\;(g+a_y)}\)

Now, \(\mathrm{m\;g = 870N \therefore\; m = \frac{870N}{g}= 88.7_8 \; kg}\)

\(\mathrm{\therefore \; F_{Ground}= 88.78 (9.80 + 16.37)= 2.32 \times 10^3 \; N}\)

This is the force  exerted by the ground on the jumper. By Newton's third law, the jumper exerts a force of equal magnitude \(\mathrm{(2.32\times 10^3 \; N)}\) on the ground.

Assume that the man remains stationary. 

(a) FBD for man:

\(\mathrm{\sum F_x = m\;a_x = 0\\ \therefore - T_A \cos \;60.0^\circ + T_B \cos \;60.0^\circ + 250 = 0 \\ \therefore \; -T_A+T_B = -500 \quad [1]\\ \sum F_y = m\; a_y = 0 \\ \therefore T_A \sin \; 60.0^\circ + T_B \sin \; 60.0^\circ - (70.0)(9.80)= 0 \\ \therefore T_A+T_B = 792._1\quad [2] \\ [1]+[2] \Rightarrow 2T_B = 292._1 \; N \; \therefore T_B= 146\;N \quad (146._1 \;N)\\ \therefore\; from\; [2],\; T_A = 646\; N}\)

(b) SImilar to (a), except \(\mathrm{T_B = 0}\) and applied \(\mathrm{F}\) is unknown.

\(\mathrm{\sum F_x = 0 \Rightarrow - T_A\; \cos \; 60.0^\circ + F = 0 \quad [3] \\ \sum F_y = 0 \Rightarrow\; T_A\; \sin \; 60.0^\circ - (70.0)(9.80)= 0 \quad [4] \\ From \; [4], \; T_A = 792._1\; N \\ Subst. \; in \; [3] \Rightarrow\; F = 396\; N}\)

(a) FBD for junction of 3 strings:

\(\mathrm{Equilibrium \Rightarrow \sum F_y = m\;a-Y = 0 \\ \therefore T_3\; \sin \; 40.06^\circ - m_B \; g = 0 \quad [1] \\ m_B\; g = 20.0\; N \Rightarrow T_3 = 31.1_1\; N \\ Then, \; \sum F_x = m\; a_x = 0 \Rightarrow T_3 \; \cos \; 40.0^\circ - T_A = 0 \quad [2] \\ \therefore \;T_A = 23.8\; N }\)

FBD for block A: 

\(\mathrm{\sum F_x = m\; a_x = 0 \Rightarrow T_A -F_f = 0 \quad [3] \\ \therefore \; F_f = T_A = 23.8\; N}\)

(b) From FBD for block A, and \(\mathrm{\sum F_y = m\;a_y = 0 \Rightarrow \; N = m_A g = 95.0 \; N}\)

Max. static friction: \(\mathrm{F_{max}= \mu_5\; N = 0.32(95.0)= 30.4\;N}\)

Similar to Eq. [3]: \(\mathrm{T_A = F_{max}= 0 \therefore T_A = 30.4\; N}\)

Eq [2] os still valid: \(\mathrm{T_3\; \cos \; 40.0^\circ - T_A = 0 \Rightarrow T_3 = 39.7\; N}\)

Eq. [1] is still valid: \(\mathrm{T_3 \; \sin \; 40.0 ^\circ - m_Bg = 0 \Rightarrow m_Bg = 26\; N}\) note that there are two significant digits (\mu_5 has two significant digits)

The crate is to be pushed in the x-direction. 

\(\therefore\) the total force must be in the x-direction. THe two forces shown have a net x-component in the \(\mathrm{+x}\) direction, and so the third force does not need an x-compnent. However, it does need a y-component so that \(\mathrm{\sum F_y = m\; a_y = 0.}\)

\(\mathrm{\therefore\; F_{1y}+ F_{2y}+F_{3y}= 0 \\ \therefore\; 130 \; \sin \; 20.0^\circ - 100\; \sin \; 50.0^\circ + F_{3y}= 0 \\ \therefore\; F_{3y}= 32.1\; N}\)

\(\therefore\) the smallest force needed is \(\mathrm{32.1\; N}\) in the y-direction.

(a)  

Use conservation of energy.

KE at top is zero.

\(\mathrm{\therefore \; \frac{1}{2}\; in \; v_o{^2}= m\; g\; y + E_{thermal}\quad [1]}\)

\(\begin {align} \mathrm{E_{thermal}} &= \mathrm{-Work\; done\; by\; friction} \\ &= \mathrm{F_Kd} \\ & = \mathrm{\mu_K Nd} \end{align}\)

But, \(\mathrm{N = m\; g\; \cos \; \theta}\) (as in Exercise 8-16, 8-17 and 8-18)

\(\mathrm{\therefore \; E_{thermal} = \mu _K m\; g\;\cos \theta \;d \\ \therefore [1] \Rightarrow \frac{1}{2} m\; v_o{^2}= m\;g\;y + \mu _K\; m\; g \cos \theta \; d}\)

Then, \(\mathrm{y=d\; \sin \theta}\)

\(\mathrm{\therefore \frac{1}{2}\; m\; v_o{^2}= m\; g\; d \; \sin \theta + \mu_K\; m\;g\cos \theta\; d\quad [2] \\ \therefore d = \frac{v_O{^2}}{2g(\sin \theta + \mu_K \cos \theta)}\\ \rightarrow d = 1.21\; m \quad (1.21_3\; m)}\)

(b) Coming down, total distance:

\(\begin {align} \mathrm{D} & = \mathrm{(1.21_3 + 2.00)m }\\ &= \mathrm{3.21_3\; m} \end {align}\)

\(\mathrm{KE\; at\; bottom = P.E. \; at\; top - E_{thermal}\\ \therefore \frac{1}{2} m\; v_f{^2}= m\; g\; D \sin \theta - \mu_K\; m\; g\; \cos \theta\; D \\ (Similar \; to \; Eq. [2])\\ \therefore v_f = \sqrt{2Dg(\sin \theta - \mu_K \cos\theta)}\\ \rightarrow v_f = 4.54\; m/s}\)

(a) Linear momentum is conserved.

\(\mathrm{\therefore m\; v_{1y}= m\; v_1{'} \; \sin 28.06\circ - m\; v_2{'} \sin 40.0^\circ \\ \therefore\; v_2{'}= \frac{\sin 28.0^\circ}{\sin 40.0^\circ} v_1{'}= 0.730_4 v_1{'}\quad [1]}\)

In x-direction \(\mathrm{m\; v_{1x}= m\; v_{1}{'}\cos 28.0^\circ + mv_2{'}\cos 40.0^\circ}\)

\(\mathrm{Subst. from \;[1] \rightarrow v_{1x}= v_1{'} \cos 28.0 +(0.730_4 v_1{'})\cos 40.0^\circ \\ where\ v_{1x} = 25.0\; m/s\\ \Rightarrow v_1{'}= 17.3\; m/s \quad (17.3_3 \; m/s)\\ [1] \Rightarrow v_2{'}= 0.730_4(17.3_3\; m/s)= 12.7\; m/s \quad (12.6_6\; m/s)}\)

(b) Fraction of KE lost

\(\mathrm{= \frac{\frac{1}{2}m\; v_1{^2}- (\frac{1}{2}mv_1{^{'2}}+ \frac{1}{2}mv_2{^{'2}} )}{\frac{1}{2}m\; v_1{^2}}\\ = \frac{v_1{^2}- (v_1{^{'2}}+ v_2{^{'2}})}{v_1{^2}}\\ = \frac{(25.0)^2 - [(17.3_3)^2+(12.6_6)^2]}{(25.0)^2}\\ = 0.263}\)

(a) Linear momentum is conserved (as in Exercise 8-21).

\(\mathrm{\therefore m_Hv_{Hx}+ m_B v_{Bx}= m_Hv_{Hx}{^{'}}+ v_{Bx}{^{'}}\\ \therefore 100(0) + (90.0)(-15.0\sin 30.0^\circ)= 100(0)+90.0v_{Bx}{^{'}}\\ \therefore v_{Bx}{^{'}}= -15.0\sin 30.0^\circ= -7.50\; m/s}\)

In y-direction:

\(\mathrm{m_Hv_{Hy}+ m_B v_{By}= m_H v_{Hy}{^{'}}+ m_Bv_{By}{^{'}}\\ \therefore 100(10.0)+(90.0)(-15.0 \cos 30.0^\circ)= 100(-3.00)+ 90.0v_{By}{^{'}}\\ \therefore v_{By}{^{'}}= 1.45_4\; m/s}\)

\(\mathrm{\Rightarrow v_B{^{'}}= 7.64\; m/s \quad (7.64_0\; m/s)\\ \theta = 11.0^\circ}\)

(b)

 \(\begin {align} \mathrm{\Delta KE}& = \mathrm{\bigg(\frac{1}{2}m_Hv_H{^{'2}}+\frac{1}{2}m_Bv_B{^{'2}}\bigg)-\bigg( \frac{1}{2}m_Hv_H{^2}+\frac{1}{2}m_Bv_B{^2} \bigg)}\\ &= \mathrm{\frac{1}{2}\bigg[ m_H(v_H{^{'2}}- v_H{^2})+m_B(v_B{^{'2}}- v_B{^2}) \bigg]} \\ & = \mathrm{\frac{1}{2}\bigg[ 100\bigg( (3.00)^2- (10.00)^2\bigg)+ 90.0 \bigg( (7.64_6)^2-(15.0)^2 \bigg) \bigg]} \\ & =\mathrm{ -1.20 \times 10^4 \; J} \end {align}\)

During any small time interval as the donkey walks, the force \(\mathrm{\overrightarrow F}\) exerted by the donkey is in the same direction as the displacement \(\mathrm{\Delta \overrightarrow r.}\)

\(\begin {align} \mathrm{\therefore \; Work \; done = W} &= \mathrm{F \Delta r \cos \theta}\\ &= \mathrm{F\Delta r \quad (\because \theta = 0)} \end {align}\)

Consider a time of 1s.

\(\begin {align} \mathrm{\Delta r = v\Delta t } &= \mathrm{\bigg( 3\;\frac{km}{h}\times \frac{1h}{3600s}\times \frac{1000m}{1km} \bigg)1s}\\ &= \mathrm{0.833_3\;m} \end {align}\)

The work done becomes grav. P.E. of the water. 

\(\mathrm{\therefore F\Delta r = m\; y\; g \\ \therefore F(0.833_3 \;m)= (100\;kg)(9.80\;m/s^2)(2.00\;m)\\ \therefore F = 2.35\times 10^3\;N}\)