Problem 8-86 Inelastic collision - Part 3B

A large ball of modeling clay \((\text{mass}\; 4.5 \times 10^2\; g)\) is rolled on a tabletop so that it collides with a stationary small wooden box \((\text{mass} \; 7.9\times 10^2\; g)\). The collision is completely inelastic, and the ball and box then slide on the table for a distance of \(5.1 \;cm\). If the speed of the ball is \(2.2\; m/s\) just before the collision, determine: (a) the speed of the ball and box just after the collision (b) the magnitude of the friction force acting on the ball and box.

Accumulated Solution

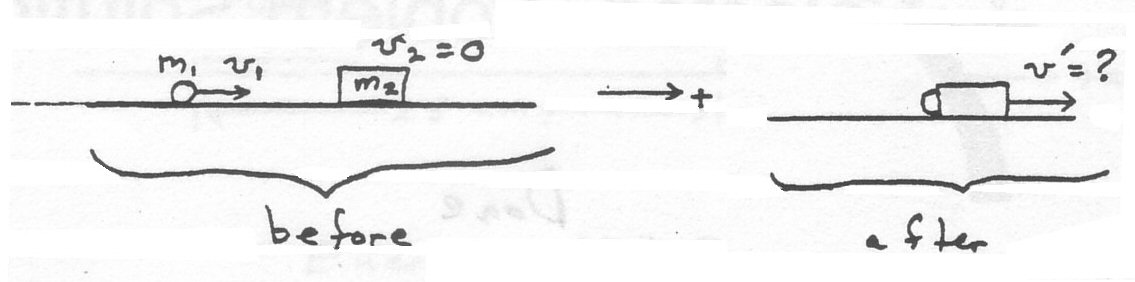
\(m_1v_1 + m_2v_2 = (m_1 + m_2)v' \quad \; \text{where}\; v_2 = 0 \\ v{'} = 0.80\; m/s\; \text{ (answer to part (a))}\)

\(v{'}= \frac{m_1}{m_1 + m_2} v_1 = \frac{4.5 \times 10^2}{12.4 \times 10^2}2.2= 0.798\; m/s = 0.80\; m/s\)

Now for part 2 of the problem we simply have an object of mass \(m = 1.24\; kg\) with an initial velocity of \(v_0 = 0.798\; m/s\) slowing down because of the force of friction. The acceleration of the mass is given by:

(A)   \(v = v_0 + at\)

(B)   \(x = v_{0^t} + (1/2)at^2\)

(C)   \(v^2 = v_0{^2} + 2ax\)