Problem 7-51 Energy cons. - Part 3 - C

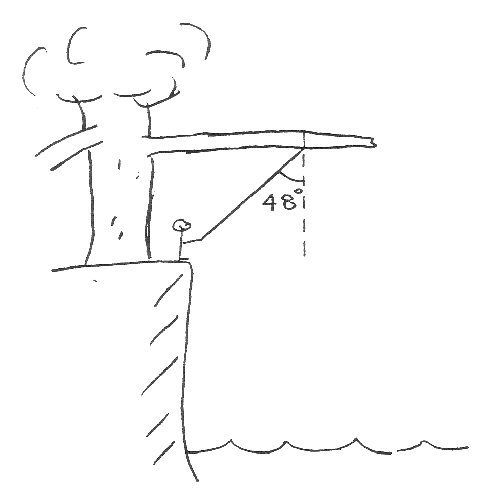
A boy is playing with a rope tied to a tree near his favourite swimming hole. Initially the boy is stationary and the rope (of length $3.7 \;m$) makes an angle of $48^\circ$ with the vertical. He then lifts his feet slightly and starts to swing freely. If air resistance is neglected, use conservation of energy to determine:

(a) his speed at the bottom of the swing
(b) the minimum height, relative to his initial position, to which he can swing.

Accumulated Solution

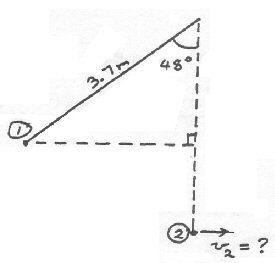
At point 2, $E_P = 0$

At point 2, $E_K = (1/2)mv^2$

Correct.

$E_K$ at point 2 is $(1/2)mv^2$

What is the height of point 1 above point 2?

(A)   $3.7\; m$

(B)   $3.7 \sin 48 \;m$

(C)   $3.7 \cos 48 \;m$

(D)   $3.7(1- \cos48)\;m$