Problem 6-53 parts (a), (b), and (c) Centripetal force - Part 6 - B

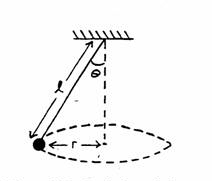
A conical pendulum consists of a mass (the bob) on the end of a string. As the bob travels in a horizontal circle at constant speed, the string traces out a cone. For the pendulum shown, mass \(m = 1.95\; kg\), length \(l = 1.03\; m\), and angle \(\theta = 36.9^\circ\).

(a) Draw a free body diagram for the bob at the instant shown.
(b) What force constitutes the centripetal force?
(c) Determine the speed of the bob.

Accumulated Solution

\(T \cos \theta = mg \\ T \ sin \theta = mv^2/r \; \;(2)\)

Correct!

Therefore:

\(\frac{\sin \theta}{\cos \theta} = \frac{v^2}{l \sin \theta g} \\ v^2 = \frac{lg \sin^2 \theta}{\cos \theta} = \frac{(1.03)(9.8)(\sin ^2 36.9^\circ)}{\cos 36.9^\circ} \\ v = 2.13\; m/s\)

This is the answer to part (c).

You have completed this problem.