Problem 4-16 - Projectile - (B)
A tennis player serves a ball horizontally, giving it a speed of \(24\; m/s\) from a height of \(2.5\; m.\) The player is \(12\; m\) from the net and the top of the net is \(0.90 \;m\) above the court surface.
(a) How long is the ball in the air, assuming it clears the net and lands in the other court?
(b) How far horizontally does the ball travel?
(c) With what velocity does the ball strike the court surface?
(d) By how much distance does the ball clear the net?
Accumulated Solution
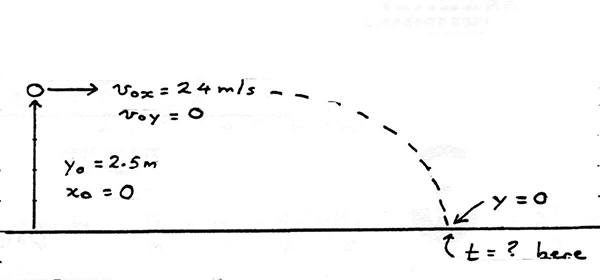
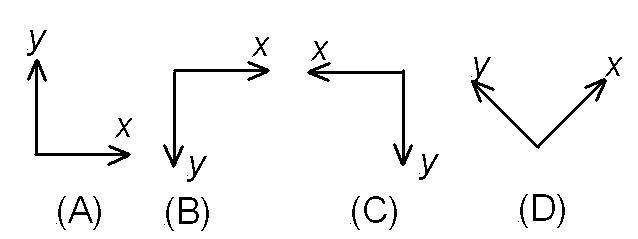
A and B are the best choice. B would make the acceleration positive but for practise we will use A in what follows. We will place the origin at the ball at \(t = 0.\)
As with all projectile we must deal with the horizontal and vertical motions separately. Let us deal with the vertical motion first.
Which of the 3 Galilean equations is useful for finding t in this case?
(A) \(v_y = v_{0y} + a_{y^t}\)
(B) \(y = v_{0_{y^t}} + (1/2)a_{y^{t^2}}\)
(C) \(v_{y^2} = v_{0_y{^2}} + 2ay\)