Problem 3-25b - Vector difference - Part 4 - (B)

Determine the vector that must be added to the sum of \(A\) and \(B\) in the figure to give a net displacement of \(4.0\; km\; \text{W}\).

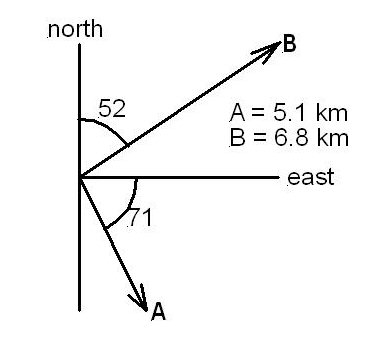
diagram indicating directions north and east as well as vectors A and B

Accumulated Solution

diagram indicating C at the desired 4 km West

Solution \(A_x\) \(B_x\) \(C_x\) \(R_x\)
(A) \(5.1 \cos 71\) \(6.8 \sin 52\) \(C_x\) \(-4\)

 

Solution \(A_y\) \(B_y\) \(C_y\) Ry
(B) \(-5.1 \sin 71\) \(6.8 \cos 52\) \(C_y \) \(0\)

\(5.1 \cos71 + 6.8 \sin52 + C_x = -4 \\ -5.1 \sin71 + 6.8 \cos52 + C_y = 0\)

\(C_x = -11\; km \\ C_y = 0.63\; km\)

Correct

\(|C| = 11\; km\)

 

The direction of \(C\) is given by:

(A)    \(\cos^{-1} C_y/C_x\)

(B)    \(\sin^{-1} C_y/C_x\)

(C)    \(\tan^{-1} C_y/C_x\)