Problem 3-25b - Vector difference - Part 4

Determine the vector that must be added to the sum of \(A\) and \(B\) in the figure to give a net displacement of \(4.0\; km\; \text{W}\).

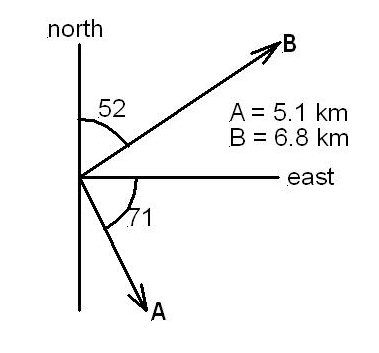
diagram indicating directions north and east as well as vectors A and B

Accumulated Solution

diagram indicating C at the desired 4 km West

Solution \(A_x\) \(B_x\) \(C_x\) \(R_x\)
(A) \(5.1 \cos 71\) \(6.8 \sin 52\) \(C_x\) \(-4\)

 

Solution \(A_y\) \(B_y\) \(C_y\) Ry
(B) \(-5.1 \sin 71\) \(6.8 \cos 52\) \(C_y\) \(0\)

\(5.1 \cos71 + 6.8 \sin52 + C_x = -4 \\ -5.1 \sin71 + 6.8 \cos52 + C_y = 0\)

You should get:
\(C_x = -11\; km \\ C_y = 0.63 \;km\)

The vector \(C\) has a length:

(A)    \(-11 + 0.63 = -10.4\; km\)

(B)    \([(-11)^2 + (0.63)^2]^{1/2} = 11\; km\)

(C)    \([(-11)^2 + (0.63)^2] = 122\; km\)