Problem 12-22 Simple circuit - Part 6 - B

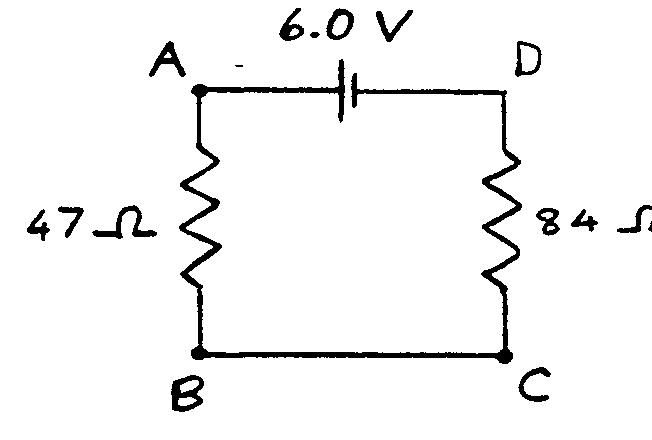
Diagram of circuit with resistors.

In the figure, what are
(a) the current through the \(47\; \Omega\) resistor?
(b) the direction of the current through the \(47\; \Omega\) resistor?
(c) the potential difference \(V_A - V_B\)?  \(V_B - V_A\)?
(d) the voltage across the \(84\;  \Omega\)  resistor?
(e) the potential at point \(C\), if we define the potential at the negative terminal of the battery to be zero?

Accumulated Solution

Circuit diagram

\(I = V/R \\ I = V/R = 6.0/131 = 0.046\; \text{A}    \quad  \text{(answer to part (a))} \\ \text{Current flows + to -, therefore A to B } \quad \text{(answer to part (b))} \\ \Delta V = IR = 0.046 \times 47 = 2.2\; V \\ V_B - V_A = -2.2 \;V  \quad    \text{(answer to part (c))} \\\)

Correct

In fact this can be determined in 2 ways:

  1. \(\Delta V = IR = (0.046)(84) = 3.8\; V\)
  2. \(\Delta V_{84} = 6 - \Delta V_{47} = 6 - 2.2 = 3.8\; V\)

(answer to part (d))

Which statement is correct?

(A)   \(V_C > V_D\)

(B)   \(V_C < V_D\)