Problem 10-31(a) Vector electric field - Part 8

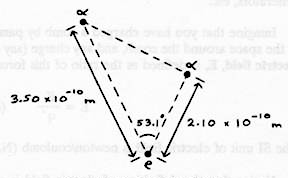
Diagram indicating the positions of two particles.

The figure shows the positions of two a particles (charge on each is \(+2e\)) and an electron. What are the magnitude and direction of
(a) the resultant force on the electron?
(Hint: choose the \(+x\) axis along the line from the electron to the right-hand a particle.)

[Ans.(a) \(1.31 \times 10^{-8} N\) at \(13.3^\circ\) to left of line from electron to right-hand a]

Accumulated Solution

Coordinate diagram B Coordinate System C .

\(F_{1x} = F_1, F_{2x} = F_2 \cos 53.1 \\ F_{1y} = 0, F_{2y} = F_2 \sin 53.1 \\ F_1 = 1.045 \times 10^{-8} N \\ F_2 = 3.76210^{-9} N\)

\(\text{Therefore} \; F_x = F_1 + F_2 \cos 53.1 = 1.045 \times10^{-8} + (0.60 \times 3.762 \times 10^{-9}) = 1.27 \times 10^{-8} N \\ \text{and,} \; F_y = 0 + F_2 \sin 53.1 = 0 + (0.80 \times 3.762 \times 10^{-9}) = 3.01 \times10^{-9} N\)

 
The magnitude of the force is given by:
 
(A)  \(F = F_1 + F_2\)

(B)  \(F = (F_1 + F_2)^{1/2}\)

(C)  \(F = F_1{^2} + F_2{^2}\)

(D)  \(F = (F_1{^2} + F_2{^2})^{1/2}\)