Problem 7-51 Energy cons. - Part 3 - C

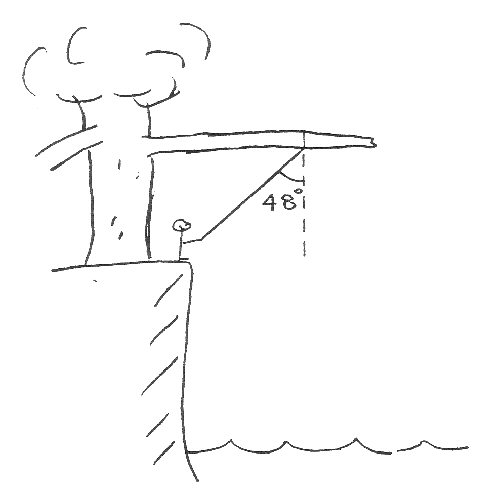
A boy is playing with a rope tied to a tree near his favourite swimming hole. Initially the boy is stationary and the rope (of length \(3.7 \;m\)) makes an angle of \(48^\circ\) with the vertical. He then lifts his feet slightly and starts to swing freely. If air resistance is neglected, use conservation of energy to determine:

(a) his speed at the bottom of the swing
(b) the minimum height, relative to his initial position, to which he can swing.

Diagram of a tree on the edge of a cliff with water below. A rope hangs from a branch hanging over the water.

Accumulated Solution

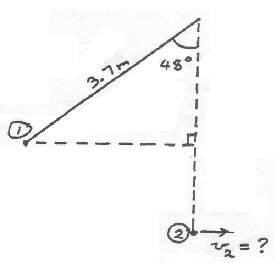
Diagram of angle of rope

At point 2, \(E_P = 0\)

At point 2, \(E_K = (1/2)mv^2\)

Correct.

\(E_K\) at point 2 is \((1/2)mv^2\)

What is the height of point 1 above point 2?

(A)   \(3.7\; m\)

(B)   \(3.7 \sin 48 \;m\)

(C)   \(3.7 \cos 48 \;m\)

(D)   \(3.7(1- \cos48)\;m\)