Biophysics Problem 4
A \(1.0\; kg\) crow sits on a telephone wire midway between two poles \(50 \;m\) apart. The wire, assumed weightless, sags by \(0.1 \;m.\) What is the tension in the wire?
To begin solving this problem, we must make a diagram of the situation labeling it with all of the information that we are given.
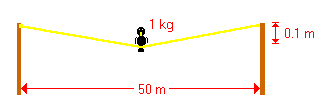
I assume your diagram is similar to this one, or at least that you understand this one. If not, see your prof or T.A.
The diagram illustrates all of the information that we are given in the problem.
Let's begin by identifying forces. What is the direction and magnitude of the force exerted by the bird on the wire?
When considering the force that the bird exerts on the wire:
- The direction of the force is down.
- The units of the magnitude are Newtons.
- The magnitude of the force in Newtons is 9.8 \(N.\)
Let's represent this force on our diagram with an arrow. The bird is exerting a force of \(9.8 \;N\) on the wire yet does not fall to the ground. Therefore, the wire must be exerting a force of \(9.8\; N\) upwards on the bird.
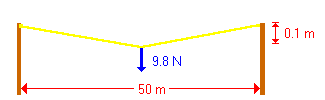
The bird's weight is being supported by the wire. I'm sure that you can see that if the wire were cut at either end, the bird would fall. This indicates that the force suppporting the bird acts in both directions from the bird along the wire, each force suppporting one half of the bird's weight.
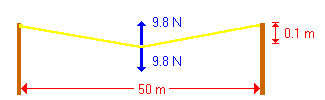
We wish to solve for this force, or tension.
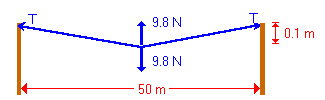
We have now illustrated all of the forces with which we are concerned. For simplicity, let's focus on one half of the wire.
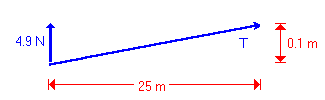
In this diagram we've focused our attention on one half of the wire. In doing this, we must divide the vertical forces by 2. Also, we can ignore the downward force of gravity.
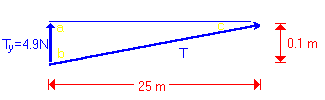
We've now reduced the problem to solving a force vector triangle. Notice that I've also labelled the angles a, b, and c. Therefore,
\(\mathrm{ T_y = T \times \sin c \\ T = T_y / \sin c}\)
We know that \(\mathrm{T_y = 4.9\; N.}\) We must determine the angle c.
We do not have enough information to calculate sin c directly, however, we know that at small angles, \(\mathrm{\tan\; c = \sin\; c.}\)
And from the diagram, \(\mathrm{\tan \;c = 0.1\;m / 25\;m.}\)
So let's calculate the tension T:
\(\mathrm{T = T_y/\sin c = T_y/\tan \;c \\ = T_y /(0.1\;m/25\; m) \\ = 4.9\; N \times 25\;m /0.1\; m \\ = 1225 \; N}\)
Therefore, the tension in the wire is \(\mathrm{1225 \;N.}\)