Biophysics Problem 18

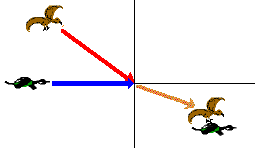
A  \(1\;kg\)  duck is flying horizontally at  \(20\; m/s\)  when seized by a  \(0.8 \;kg\)  hawk diving down at  \(30\; m/s.\)  The hawk is coming in from behind and makes an angle of  \(30^\circ\)  from the vertical just before contact. What is the velocity of the birds just after contact?

Recognize that this is a problem on conservation of momentum in two dimensions.

Let's first begin by labelling all the known angles and velocities.

diagram illustrating all known angles and velocities

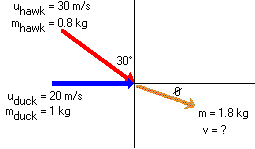
diagram illustrating all angles and velocities

You will have to establish an equation for conservation of momentum in each of the vertical and horizontal directions.

Before you can do this you must represent all velocities by their vertical and horizontal components.

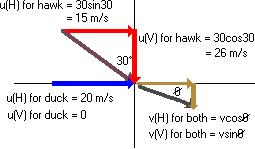
diagram illustrating conservation of momentum for each angle and direction
Now you are ready to write down an equation for conservation of momentum in each of the two directions.

Remember, in each equation the momentum before the collision must equal the momentum after the collision (in that direction).

Write out the equations now.

In the horizontal (or \(x\)) direction:

\(\text{Total}\; 'x'\; \text{momentum before} = \text{Total}\; 'x' \; \text{momentum after} \\ m_{duck} u_{duck, x} - m_{hawk} u_{hawk, x} = (m_{duck} + m_{hawk}) v_{both,x} \\ (1\; kg \times 20\; m/s)+(0.8\; kg \times 15 \; m/s) = (1.8 \; kg \times \cos \theta) \\ 32\; kg \; m/s = (1.8\; kg \times \cos \theta)\)

And in the vertical (or \(y\)) direction:

\(\text{Total}\; 'x'\; \text{momentum before} = \text{Total}\; 'x' \; \text{momentum after} \\ m_{duck} u_{duck, x} - m_{hawk} u_{hawk, x} = (m_{duck} + m_{hawk}) v_{both,x} \\ (0.8\; kg \times 26 \; m/s) = (1.8 \; kg \times \sin \theta)\)

So we now have two equations with two unknowns.


All that is left is to solve for \('v' \; \text{and}\; ' \theta'.\) (First, find \(\theta\), then \(v\)).